Motivation

The scaling of the bulk Si MOSFET beyond the 45 nm technology node is extremely difficult due to (i) a low Si mobility and (ii) quantum-mechanical tunnelling through the sub-1 nm thin gate oxide which results in an intolerably high leakage. Therefore, it is widely accepted that the bulk MOSFET architecture has to be dramatically changed and the industry is adopting non-orthodox materials, new technologies and alternative device architectures. Naturally, the research into alternative transistor architectures recreated the possibility of building MOSFET based on III-V materials [1] to profit from a higher mobility in the channel. The development of suitable high-κ gate dielectrics for GaAs with an unpinned oxide/semiconductor interface [2] is recognised as the most important step towards a real III-V transistor as depicted in Fig. 1.

Background

Past objections to III-V technologies:

• III-V materials do not have a good native oxide;
• III-V devices have to be grown by epitaxial technology;
• III-V substrates are not in large diameters to offer competitive economies of scale;
• III-V transistors cannot be integrated within the current Si based technology.

Today, industry is already adopting non-orthodox materials and technologies, such as:

• high-κ dielectrics for GaAs/AlGaAs with unpinned oxide/semiconductor interface by Freescale Semiconductor;
• epitaxial SiGe in CMOS;
• alternative device architectures.

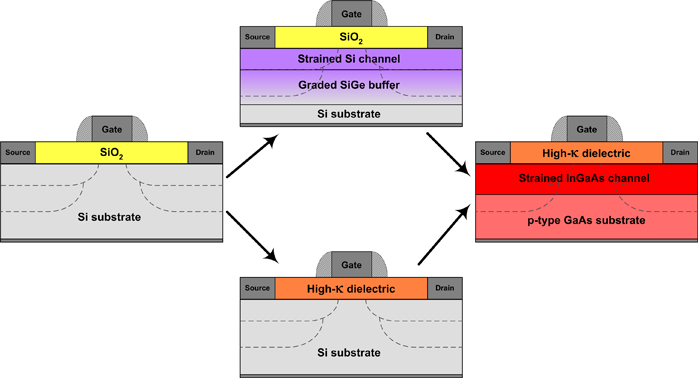Fig. 1: Evolution of technology. The design of the bulk Si MOSFET undergoes changes by replacing SiO2 with high-κ or by replacing Si in the channel with strained Si grown on the graded SiGe buffer. Further improvement in the channel mobility is possible by replacing the strained Si in the channel by the strained InGaAs grown on GaAs buffer.

Overview

Monte Carlo device simulations show [1,3] that the equivalent III-V MOSFET transistor would outperformed the Si and strain Si MOSFETs when scaled down to a metallurgical gate length of 30 nm but its performance will deteriorate in sub-30 nm dimensions. This decline in performance is associated with a low density of states in III-V materials compared with that of Si and Ge.

Modelling approach

We have studied the potential performance of an n-type InGaAs channel MOSFET with an 80 nm physical gate length and a high-κ gate dielectric as depicted in Fig. 2 using ensemble Monte Carlo simulator MC/MOS. We have extended our transport model [4] by using Fermi-Dirac statistics for the screening in ionized impurity scattering and Fermi exclusion principle (degeneracy) at each scattering process [5] . Further, we have incorporated a roughness scattering at the oxide/semiconductor interface and adopted the effective quantum potential to incorporate the effect of quantum confinement. The simulated performance of the InGaAs channel MOSFETs is then compared with the results for equivalent n-type conventional and strained Si channel MOSFETs which have been obtained from calibrated Monte Carlo simulations in order to fairly compare the intrinsic device performance.

Features of the Monte Carlo device simulator MC/MOS:

• Finite elements used to depict the complex geometry.
• Analytical non-parabolic band structure with 3 valleys.
• Scattering mechanisms: electron interaction with acoustic phonons, polar optical phonons, non-polar optical phonons (intravalley and intervalley), ionized and neutral impurity scatterings.
• In the InGaAs channel the effect of alloy scattering and the effect of strain on bandgap, electron effective masses, potential and energy of optical phonons are considered.
• Interface roughness.
• Fermi-Dirac statistics.
• Quantum confinement corrections.

Design of equivalent bulk InGaAs MOSFETs

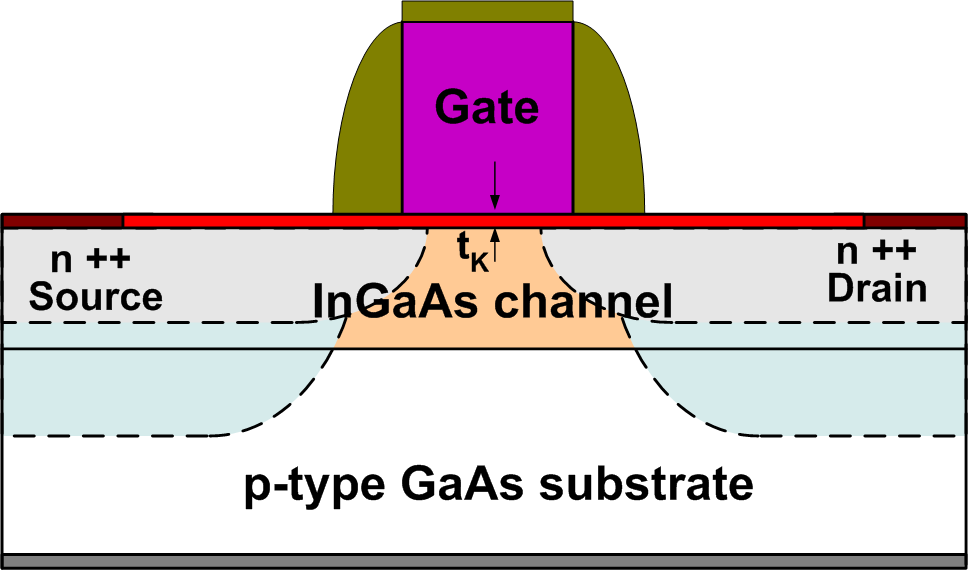Fig. 2: Cross-section of the 80 nm gate length In0.2Ga0.8As MOSFET considered in Monte Carlo simulations.

The layout of the In_0.2Ga_0.8As channel MOSFETs on GaAs buffer mimics the structure and equivalent oxide thickness of the 67 nm effective channel length n-type Si based MOSFETs published by IBM and the 35 nm Si MOSFET developed by Toshiba. However, the doping profiles for the equivalent InGaAs MOSFETs have to be adjusted to reflect the technologically possible range of doping concentrations for III-V materials since the sub-100 nm Si MOSFETs use high doping concentrations in the source/drain regions in order to reduce an access resistance thus achieving large drive currents. Fig. 2 shows InGaAs MOSFETs with a metallurgical gate length of 80 nm which is designed to have the same junction depth as the 67 nm effective channel length n-type bulk and strained Si MOSFETs. Moreover, we used process simulations to design equivalent 35 nm metallurgical gate length InGaAs MOSFETs to compare their performance with the 35 nm Si MOSFET. We have designed two possible doping profiles for the InGaAs MOSFETS, one with the peak doping of 5×10¹⁹ cm^-3 shown in Fig. 3 for the 80 nm gate length In_0.2Ga_0.8As MOSFETs and in Fig. 7 for 35 nm metallurgical gate length InGaAs MOSFETs which represents a maximum possible doping. We have also considered the peak doping of 2×10¹⁹ cm^-3 representing a more realistic value which can be achieved by today's technology.

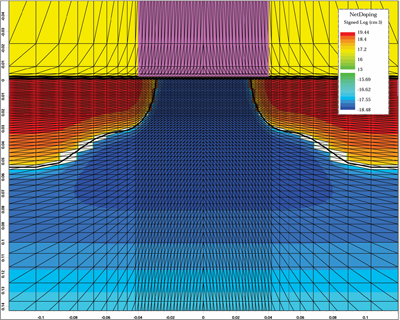Fig. 3: Doping profile with a peak doping of 5×1019 cm-3 for the 80 nm gate length In0.2Ga0.8As MOSFET considers also the extension regions.

Performance of the 80 nm gate length In_0.2Ga_0.8As MOSFETs

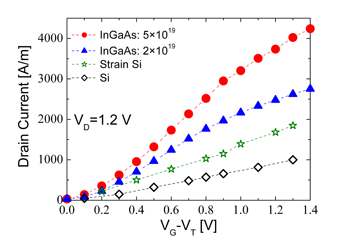
Figures 4 and 5 show I_D-(V_G-V_T) characteristics at drain voltages of 0.1 V and 1.2 V, respectively, for the 80 nm InGaAs MOSFETs. The devices with a source/drain doping of 5×10¹⁹ cm^-3 would outperform by more than 300% the equivalent strained Si MOSFET at a low drain voltage of 0.1 V. This is reduced to 65% when the source/drain doping is 2×10¹⁹ cm^-3 which is more realistic for the current technology. At a high drain voltage of 1.2 V the 80 nm InGaAs MOSFETs still outperforms the strained Si MOSFET by more than 200% when the peak doping in the source/drain is 5×10¹⁹ cm^-3 and by about 50% when this is 2×10¹⁹ cm^-3.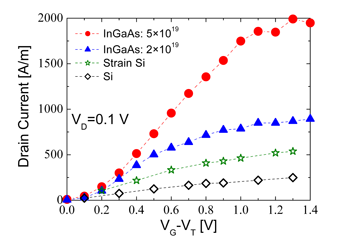

Fig. 4: ID-(VG-VT) characteristics of the 80 nm In0.2Ga0.8As MOSFET at a low drain voltage VD=0.1 V compared with the 80 nm Si and strained Si MOSFETs (both have a 67 nm effective channel length). The full circles are for the InGaAs MOSFET with a peak doping of 5×1019 cm-3 while the full triangles are for a peak doping of In0.2Ga0.8As.		Fig. 5: ID-(VG-VT) characteristics of the 80 nm In0.2Ga0.8As MOSFET at a high drain voltage VD=1.2 V compared with the 80 nm Si and strained Si MOSFETs. The full circles are for the InGaAs MOSFET with a peak doping of 5×1019 cm-3 while the full triangles are for a peak doping of In0.2Ga0.8As.

The average velocity along the InGaAs channel shown in Fig. 6 is much higher than that in the Si and strained MOSFETs. This is thanks to a lower effective mass of electrons entering the channel predominantly in the Γ-valley and also thanks to the reduced phonon scattering. The peak velocity in the 80 nm InGaAs MOSFET with a doping of 2×10¹⁹ cm^-3 is about 95% larger than the peak electron velocity in the equivalent 80 nm strained Si MOSFET. When the peak doping in the source/drain is further increased to 5×10¹⁹ cm^-3 the peak average electron velocity can achieve 130% increase compared to the peak velocity in the strained Si MOSFET. The peak of the average electron velocity in the 80 nm InGaAs MOSFET is shifted more to the source side of the device when compared to the peak in both Si MOSFETs indicating that an electron can gain a high energy faster when entering the channel. The high energy electron has higher probability of being transfered into the upper valleys (L and X) with larger effective masses where their movement becomes slower. In addition, the phonon scattering in the upper valleys is also enhanced compared to the Γ-valley. Thus these high energy electrons begin to lose energy and their velocity drops down much faster than the velocity in the equivalent Si devices.

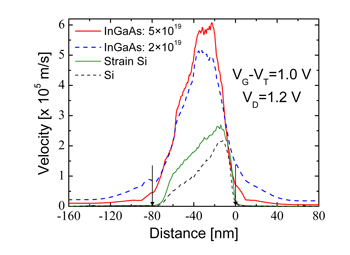Fig. 6: Average electron velocity along the 80 nm gate length In0.2Ga0.8As channel MOSFETs with the indicated source/drain doping shown by thick full and dash lines compared with the velocity in the equivalent strained Si and Si MOSFETs shown by thin lines. The arrows depict the beginning and the end of the physical gate.

The situation changes when InGaAs and Si MOSFETs are scaled down to the 35 nm physical gate length.

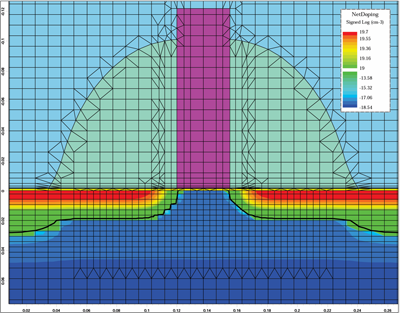Fig. 7: Doping profile with a peak doping of 5×1019 cm-3 for the 35 nm gate length In0.2Ga0.8As MOSFET obtained from Taurus process simulations.

Performance of the 35 nm gate length In_0.2Ga_0.8As MOSFETs

The 35 nm InGaAs MOSFET cannot outperform the equivalent strained Si MOSFETs with more than a 10% Ge content virtual substrate as shown by their I_D-(V_G-V_T) characteristics in Figs. 8 and 9 at both low and high drain voltages, respectively. The 35 nm In_0.2Ga_0.8As MOSFET with a peak doping of 2×10¹⁹ cm^-3 is not able to compete even with the bulk 35 nm Si MOSFET. The 35 nm In_0.2Ga_0.8As MOSFET with a peak doping of 5×10¹⁹ cm^-3 can outperform the bulk 35 nm Si MOSFET by just 24% while it is outperformed by both strained Si MOSFETs with 10% and 15% Ge content virtual substrates. This performance decline is attributed to a relatively low density of states in In_0.2Ga_0.8As channel materials when compared to the density of states of Si or Ge. The other factor which is also important is that the n-type doping in the source/drain of the III-V MOSFETs has to be much lower due to technological restrictions than the extremely high doping which can be applied in the equivalent Si and Ge MOSFETs. We would also like to note that the doping designs of both the 80 nm and 35 nm InGaAs MOSFETs have been kept as close as possible to the doping profiles of Si based devices. The performance of the 35 nm InGaAs MOSFETs could be improved if the doping profile would be optimised for the lower density of states in III-V materials.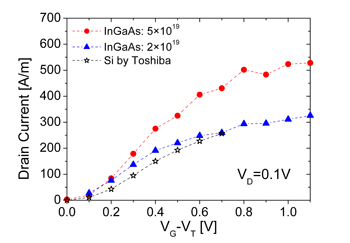

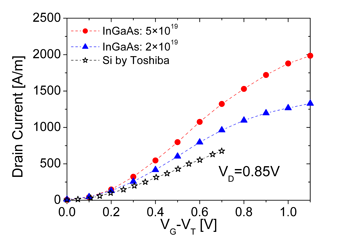
Fig. 8: ID-(VG-VT) characteristics of the 35 nm In0.2Ga0.8As MOSFET at VD=0.1 V compared with experimental date obtained from the 35 nm gate legnth Si MOSFETs. The two variants of the 35 nm InGaAs MOSFET with peak dopings of 5×1019 cm-3 and 2×1019 cm-3 are shown.		Fig. 9: ID-(VG-VT) characteristics of the 80 nm In0.2Ga0.8As MOSFET at VD=0.85 V compared with the 35 nm gate legnth bulk Si MOSFET. The full circles are for the InGaAs MOSFET with a peak doping of 5×1019 cm-3 while the full triangles are for a peak doping of In0.2Ga0.8As are again presented.

Conclusions on scaling of the bulk InGaAs MOSFETs

Using ensemble Monte Carlo device simulations we have demonstrated that compound 80 nm MOSFETs with an In_0.2Ga_0.8As channel may deliver significant improvement in the drive current compared to the present state of the art bulk and strained Si channel MOSFETs. We have found that the 80 nm InGaAs MOSFET with a source/drain doping of 2×10¹⁹ cm^-3 would outperform the equivalent Si MOSFET by more than 60% and even by 200% when the source/drain doping is increased to 5×10¹⁹ cm^-3 at both low and high drain voltages. We have attributed the improvement reported in this work to improved device design and particularly the use of optimal n-type doping in the source/drain and background p-type doping in the design of the InGaAs MOSFET. However, the situation changes for the 35 nm InGaAs MOSFET which cannot outperform the equivalent strained Si MOSFETs with more than a 10% Ge content virtual substrate at any drain voltages even when the extremely high source/drain peak doping of 5×10¹⁹ cm^-3 is applied. This is attributed to a low density of states in In_0.2Ga_0.8As channel compared to the density of states in Si and agrees with results reported in Ref. 4.

Implant free In_0.25Ga_0.75As III-V MOSFETs

The introduction of III-V materials in MOSFETs requires new device concepts which enable full exploitation of the high mobility in the scaling process. The new device concept proposed by Frescale Semiconductor [6] is an enhancement mode MOSFET with implant free source/drain regions as shown in Fig. 9. This device contains a buried, high mobility channel formed in a quantum well with energy barriers comparable to the supply voltages at and beyond the 22 nm node. In this way, the carriers are well confined to the channel, providing ultra-thin body like scaling performance. In the access regions, the carriers are supplied to the channel from a doping plane, obviating the need for implanted contact formation and overcoming thermal budget issues associated with efficient implant activation. This results in the carriers being injected at the source side of the gate from a high mobility region, with high velocity and low back-scattering producing very high drive current. The doping strategy is such that the resistance of the access regions either side of the gate is low, whilst under the gate, the structure is normally off, controlled by the work-function of the metal gate. Due to excellent electrostatic integrity and very high channel mobility, the proposed structure tolerates relatively thick gate oxide even at very short gate lengths. This mitigates the impact of the low III-V density of states sustaining very high drive current in nano-scale devices at very low supply voltage.

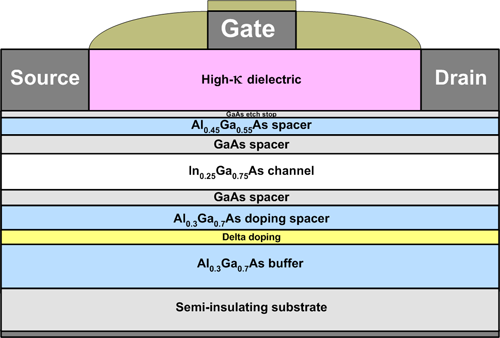Fig. 9 n-type implant free In0.25Ga0.75As MOSFET with a gate length of 100 nm MOSFET considered in Monte Carlo simulations.

We have performed a study of the potential performance of the implant free In_0.25Ga_0.75As MOSFET proportionally scaled from a gate length of 100 nm to 70 nm and 50 nm. In order to maintain the electrostatic integrity in the 100, 70 and 50 nm gate length transistors, the oxide thickness is scaled to 18, 13, and 9 nm and the In_0.25Ga_0.75As channel thickness is scaled to 10, 7 and 5 nm, respectively. The active δ-doping concentration was also increased from 2.65×10¹² cm^-2 to 3.5×10¹² cm^-2 and to 4.25×10¹² cm^-2, respectively. Finally, we would like to stress that the predicted performance of all implant free InGaAs MOSFETs corresponds to an intrinsic devices which means that the impact of the external contact resistances is neglected. Figure 10 presents the conduction band profile and electron density obtained from the 1D self-consistent solution of the Poisson-Schrodinger equations. The peak of the electron density steadily increases as the layer heterostructure is scaled from a gate length of 100 nm to 70 and 50 nm, respectively. In addition, the electron sheet density as a function of applied gate bias also increases with the scaling as shown in Fig. 11 where both results obtained from 1D Poisson and Poisson-Schrodinger simulations are plotted.

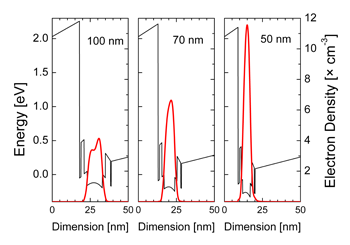
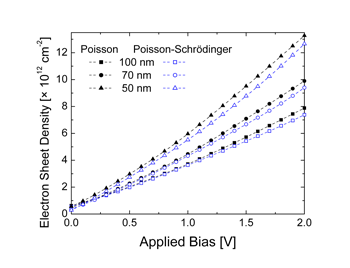
Fig. 10: Conduction band and electron density in the 100 nm, 70 nm and 50 nm implant free MOSFETs at VG-VT=0.5 V.		Fig. 11: Electron sheet density versus difference between the applied bias and threshold voltage for the 100 nm, 70 nm and 50 nm gate length MOSFETs. The results obtained using both Poisson and Poisson-Schrodinger solutions are shown.

The electron drift mobility obtained from the MC simulations has been verified against room temperature mobility measurements of an implant-free In_0.25Ga_0.75As MOSFET layer structure performed on gated Hall structures. The sheet carrier density obtained from these measurements was used to calibrate the active δ-doping concentration in the device heterostructure. Finally, we would like to stress that the predicted performance of all implant free InGaAs MOSFETs is obtained for an intrinsic device what means that an impact of external contact resistances is neglected. Figure 12 shows I_D-V_G characteristics for different drain biases (V_D) for a 100 nm gate length implant free In_0.25Ga_0.75As with 100 nm source-to-gate and gate-to-drain separations. The full symbols represent the drain current obtained using Boltzmann statistics and Debye-Huckel screening for ionized impurity scattering while the open symbols show results obtained using the self-consistent Fermi-Dirac statistics. The drain current as a function of the gate voltage rapidly increases when the gate voltage changes from 0.1 V to 0.3 V. The increase is reduced at a gate voltage of 0.5 V and eventually, I_D saturates at V_G=0.7 V.

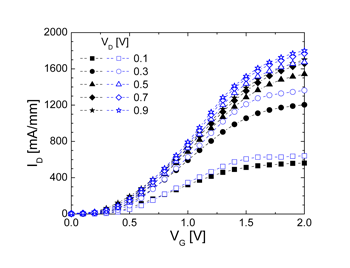Fig. 12: ID-VG characteristics for different drain voltages (VD) of the 100 nm gate length implant free In0.25Ga0.75As MOSFET. The full symbols show the drain current obtained using Boltzmann statistics while the open symbols are results obtained using self-consistent Fermi-Dirac statistics. The source-to-gate and the gate-to-drain distances are set to 100 nm.

The scaling potential of the implant free In_0.25Ga_0.75As MOSFET has been evaluated as well. In order to do so we have scaled the 100 nm gate length implant free In_0.25Ga_0.75As MOSFET in both vertical and lateral directions with respect to gate lengths of 70 nm and 50 nm. Figure 13 shows I_D-V_G characteristics for the 70 nm gate length implant free In_0.25Ga_0.75As. The results obtained using Boltzmann statistics (full symbols) as well as using Fermi-Dirac statistics (open symbols) are compared. The drain current increases by about 50% as a results of the device scaling compared to the drain current delivered by the 100 nm implant free In_0.25Ga_0.75As MOSFETs. A further increase of 90% in the drain current can be observed in Fig. 13 which shows I_D-V_G characteristics for the 50 nm gate length implant free In_0.25Ga_0.75As MOSFET. Both results obtained using Boltzmann statistics and Fermi-Dirac statistics are again presented. Figs. 13 and 14 demonstrate that the implant free In_0.25Ga_0.75As MOSFET can be effectively scaled and that large performance improvements can be obtained through device scaling. It further becomes apparent from Figs. 13 and 14 that the difference between Fermi-Dirac and Boltzmann statistics increases with increasing drain voltage and that Fermi-Dirac statistics give a slightly larger drain current by about 12% (at V_D=0.3 V) for the 100 nm and 70 nm gate lengths MOSFETs. In the case of the 50 nm gate length In_0.25Ga_0.75As MOSFET, the effect of Fermi-Dirac statistics becomes negligible since the difference between the drain current obtained using Boltzmann statistics and using Fermi-Dirac statistics is only 5%.

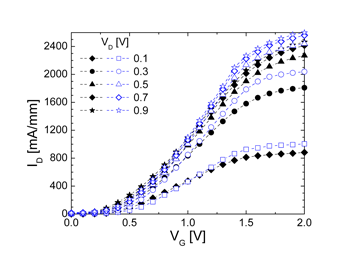
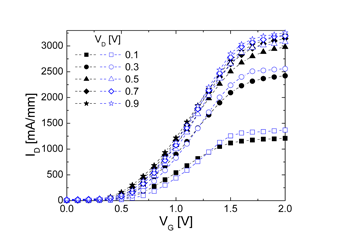
Fig. 13: ID-VG characteristics for different VD of the 70 nm gate length implant free In0.25Ga0.75As MOSFET. The full symbols show the drain current obtained using Boltzmann statistics and the open symbols using Fermi-Dirac statistics. The source-to-gate and gate-to-drain distances are also scaled to 70 nm.		Fig. 14: ID-VG characteristics for different VD of the 50 nm gate length implant free In0.25Ga0.75As MOSFET. The full symbols represent results of MC simulations using Boltzmann statistics and the open symbols using self-consistent Fermi-Dirac statistics. The source-to-gate and the gate-to-drain distances are 50 nm.

Finally, the average electron velocity along the In_0.25Ga_0.75As channel in scaled implant free MOSFETs with gate lengths of 100 nm, 70 nm and 50 nm is presented in Fig. 15. Electrons travelling through the channel quickly gain a large velocity which peaks at 4.8× 10⁵ m/s in the 100 nm device when the MC simulations are run using Boltzmann statistics and at 5.08× 10⁵ m/s when using Fermi-Dirac statistics. When the device is proportionally scaled down to gate lengths of 70 nm and 50 nm the electron peak velocity further increases to 5.4× 10⁵ m/s (5.7× 10⁵ m/s) and 5.6× 10⁵ m/s when using Boltzmann statistics (6.0× 10⁵ m/s when using Fermi-Dirac statistics), respectively. The velocity increase becomes less in the scaled devices because the benefit of the improved non-equilibrium electron transport is partially suppressed by enhanced scattering due to higher δ-doping concentrations.

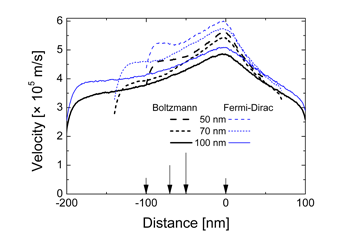Fig. 15: Average electron velocity along the In0.25Ga0.75As channel of scaled implant free MOSFETs with indicated gate lengths at VG-VT=1.3 V and VD=0.7 V. The thick lines are results obtained from MC simulations using Boltzmann statistics while the thin lines are results when Fermi-Dirac statistics is used. The beginning of the gate is depicted by arrows while the end of the gate is always set at zero.

Conclusions on scaling of the implant free InGaAs MOSFETs

Using ensemble Monte Carlo device simulations we have demonstrated that a 100 nm implant free MOSFET with an In_0.25Ga_0.75As channel exhibits an excellent drive current of 1650 mA/mm and a maximum transconductance of 1340 mS/mm obtained with a small supply voltage. The MC device simulations have been carefully implemented by:

calibrating the bulk MC transport model against experimental data obtained for bulk GaAs, AlGaAs and InGaAs;

verifying the ensemble MC device simulator against experimentally obtained I_D-V_G characteristics of HEMTs and, most importantly;

verifying the simulated electron mobility and sheet density in the implant free In_0.25Ga_0.75As MOSFET against measured data obtained from epitaxial layers.
The implant free In_0.25Ga_0.75As MOSFET has also shown excellent scaling potential. The 70 nm gate length implant free In_0.25Ga_0.75As MOSFET which is properly scaled in both vertical and lateral directions can deliver a drain current increase of about 50-60% and a maximum transconductance of 2080 mS/mm. When the device is further scaled down to a 50 nm gate length, the drain current increases by about 90-100% compared to the drain current observed in the 100 nm implant free MOSFET and a maximum transconductance of 3190 mS/mm may be achieved.

REFERENCES:

[1] K. Kalna, M. Boriçi, L. Yang and A. Asenov, Monte Carlo simulations of III-V MOSFETs, Semicond. Sci. Technol. 19 S202-S205 (2004).
[2] Z. Yu, C. D. Overgaard, R. Droopad, M. Passlack, and J. K. Abrokwah, Growth and physical properties of Ga₂O₃ thin films on GaAs(001) substrate by molecular-beam epitaxy, Appl. Phys. Lett. 82 2978-2980 (2003).
[3] M. V. Fischetti, S. E. Laux, P. M. Solomon and A. Kumar, Thirty Years of Monte Carlo Simulations of Electronic Transport in Semiconductors: Their Relevance to Science and Mainstream VLSI Technology, J. Comput. Electron. 3, 287-293 (2004).
[4] K. Kalna, S. Roy, A. Asenov, K. Elgaid, and I. Thayne, Scaling of pseudomorphic high electron mobility transistors to decanano dimensions, Solid-State Electron. 46 (no. 5) 631-638 (2002).
[5] K. Kalna, L. Yang and A. Asenov, Monte Carlo simulations of sub-100 nm InGaAs MOSFETs for digital applications, in Proceedings of ESSDERC 2005, ed. by G. Ghibaudo, T. Skotnicki, S. Cristoloveanu and M. Brillouët, pp. 169-172 (Grenoble, France, 2005).
[6] M. Passlack, O. Hartin, M. Ray, N. Medendorp, "US Patent Publication," No. 2004-0137673, July 15, 2004.

Copyright © karolkalna