Professor Sondipon Adhikari (FRAeS)
Chair of Aerospace Engineering
College of Engineering, Swansea University
Bay Campus, Fabian Way, Crymlyn Burrows
Swansea, SA1 8EN, United Kingdom
Phone: + 44 (0)1792 602088, Fax: + 44 (0)1792 295676
Email: S.Adhikari@swansea.ac.uk, Sondipon.Adhikari@gmail.com
| Digital twins and inverse problems | ||||||||||||||||
 Figure: A word-cloud from the title of the journal papers Unlike the 'forward problem' the class of inverse problem is generally ill-posed problem and consequently considered as more difficult. Professor Adhikari's research works in this field contribute to the following sub areas:
D.1. Nanomechanical sensorsLabel-free mass sensing using cantilever-like resonators is an active field of multidisciplinary research. Depending on the size on the cantilever, the mass to be detected can vary from few atoms to relatively larger size like DNA and other biological molecules. With the advancement of manufacturing technology, micrometre-size cantilever sensors are expected to be used in practice in the near future for a variety of applications including biosensors, environmental sensor, gas sensors and chemical sensors. For any mechanical sensors to work in a reliable manner, it is necessary that the object to be sensed makes a detectable change in a quantity which can be measured easily and accurately. The measurement of the resonance frequency is one of the most fundamental properties of an oscillator and can be measured reliably across a wide range of mechanical systems. Resonance based sensors offer the significant potential of achieving the high-fidelity requirement of many sensing applications. This is essentially an inverse problem where the mass needs to be identified from a detectable change. Our research developed novel analytical formulation to solve the inverse problem using energy principles. This not only reduces the computational time but also improves physical understandings. We also proposed a completely new way for mass sensing using a shift in the damping factors of the system, enhancing the only existing possibility of using the frequency shift.
Key Journal Publications
D.2. Identification of nonlinear systemsThe inverse problem of estimating time-invariant (static) parameters of nonlinear systems is considered in this research. The state and parameter estimates of systems exhibiting oscillation obtained from noisy observational data provide valuable information for assessing the safety and reliability of the engineering system in its operational state. The parameter estimation problem falls in the general category of system identification. We explore the feasibility of joint state and parameter estimation of noise-driven chaotic systems using the extended Kalman filter (EKF), ensemble Kalman filter (EnKF), and particle filter (PF). We consider the chaotic vibration of a noisy Duffing oscillator perturbed by combined harmonic and random inputs ensuring a transition probability density function (pdf) of motion which displays strongly non-Gaussian features. Our system offers computational simplicity while exhibiting a kaleidoscope of dynamical behaviour with a slight change of input and system parameters. An extensive numerical study is undertaken to contrast the performance of various nonlinear filtering algorithms with respect to the sparsity of observational data and strength of model and measurement noise.
Key Journal Publications
D.3. Model updating and damage detectionSystem identification plays a crucial role in the model-based prediction of dynamical systems. A finite representation of a continuous media described by a partial differential equation usually leads to a discrete dynamical system. In practical applications involving linear continuous operators, the discrete system is fully characterised by the so-called mass, stiffness and damping matrices. Once these matrices are estimated with reasonable confidence, such discrete model can predict the response of the underlying dynamical system to external disturbances. In the context of structural dynamics, the identification of these system matrices is achieved by traditional modal analysis techniques. In the low-frequency domain, only a few modes contribute to the total response of the system. Experimental modal analysis permits the extraction of such modal parameters through experimental measurements. However, there are uncertainties in the measured data and also in the modelling approaches. Our vision is to develop probabilistic model updating to address this issue. We also use spectral methods for system identification and damage detection for high-frequency applications.
Book
D.4. Identification of dampingCharacterisation of damping forces in a vibrating structure has long been an active area of research in structural dynamics. The demands of modern engineering have led to a steady increase of interest in recent years. However, in spite of a large amount of research, understanding of damping mechanisms is still quite primitive. A major reason for this is that, by contrast with inertia and stiffness forces, it is not in general clear which state variables are relevant to determine the damping forces. By far the most common approach is to assume so-called 'viscous damping', a linear model in which it is supposed that the instantaneous generalised velocities are the only relevant state variables that determine damping. This approach was first introduced by Rayleigh in 1877 via his famous 'dissipation function', a quadratic expression for the energy dissipation rate with a symmetric matrix of coefficients, the 'damping matrix'. A further idealisation, also pointed out by Rayleigh, is to assume the damping matrix to be a linear combination of the mass and stiffness matrices. Rayleigh was quite clear that this idea was suggested for mathematical convenience only, because it allows the damping matrix to be diagonalised simultaneously with the mass and stiffness matrices, preserving the simplicity of uncoupled, real normal modes as in the undamped case. Since its introduction, this model has been used extensively and is now usually known as 'Rayleigh damping', 'proportional damping' or 'classical damping'.Unfortunately, there is no physical reason why a general system should behave like this. In fact, practical experience in modal testing shows that most real-life structures do not do so, as they possess complex modes instead of real normal modes. As Sestieri and Ibrahim (1994) have put it '... it is ironic that the real modes are in fact not real at all, in that in practice they do not exist, while complex modes are those practically identifiable from experimental tests. This implies that real modes are a pure abstraction, in contrast with complex modes that are, therefore, the only reality!' However, consideration of complex modes in the experimental modal analysis has not been very popular among researchers. Our work uses complex modes to identify a realistic model of damping. Both viscous and non-viscous damping modes are considered. New identification methods have been proposed and independently validated.
Book
D.5. Digital twinA digital twin is an avatar of a real physical system which exists in the computer. While a computer model of a physical system attempts to closely match the behaviour of a physical system, the digital twin also tracks the temporal evolution of the physical system. The recent rise of digital twins motivated academic and industrial researchers to formalise and standardise underlying procedures and methodologies. We clearly see the benefit of such an approach due to the possibility of wider adoption of digital twins across several industrial sectors. However, a major drawback of such an approach is jargon-dominated literature, which many early adopters of digital twins may find it difficult to tailor for their specific application sector. Keeping this background in mind, we propose a specific but original approach to develop digital twins for structural dynamic systems. Our main scientific proposition is that the digital twin evolves at a time-scale which is much slower than the dynamics of the system. This makes it possible to identify crucial system parameters as a function of the `slow-time' from continuously measured data.
This page was by Sondipon Adhikari |
||||||||||||||||
Bending mode of a CNT with a bio molecule
Local mode of a CNT with a bio molecule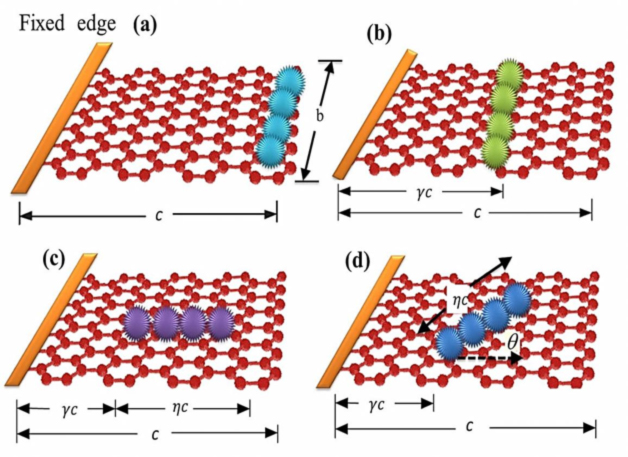
Graphene based nanomechanical sensors
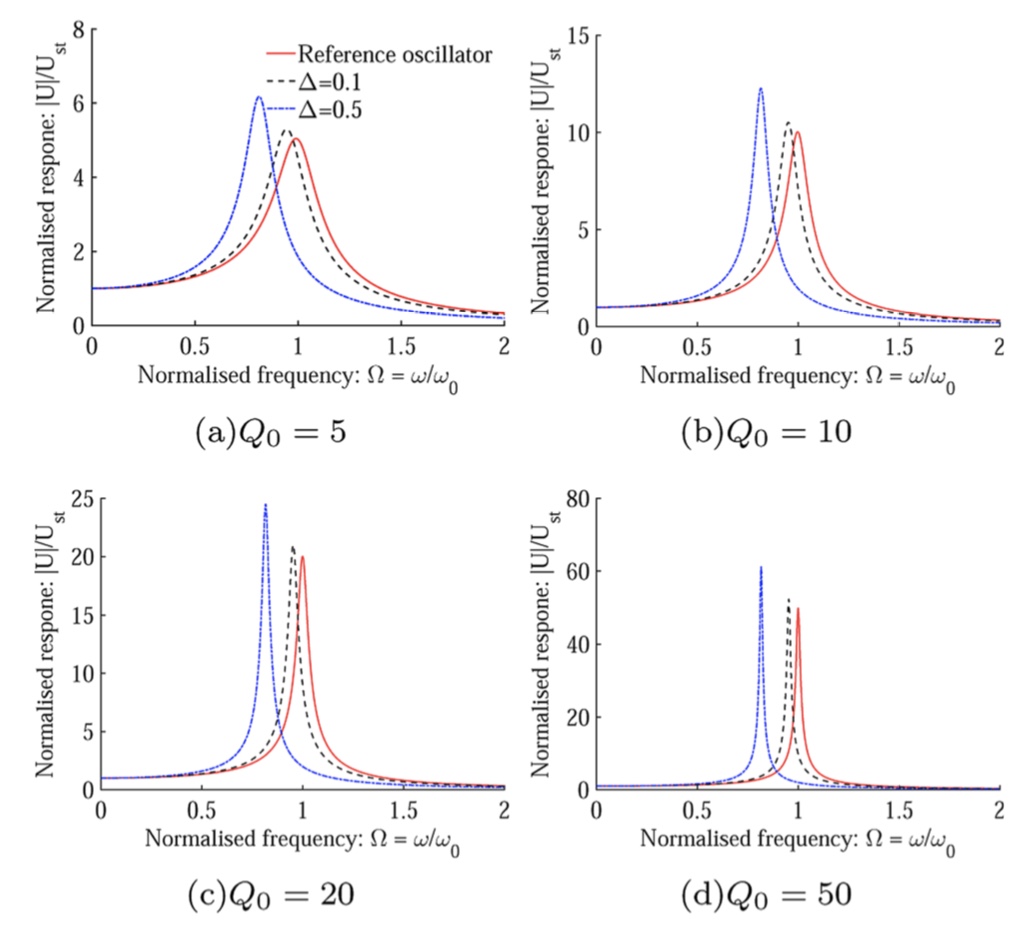Damping factor shift in cantilever sensors
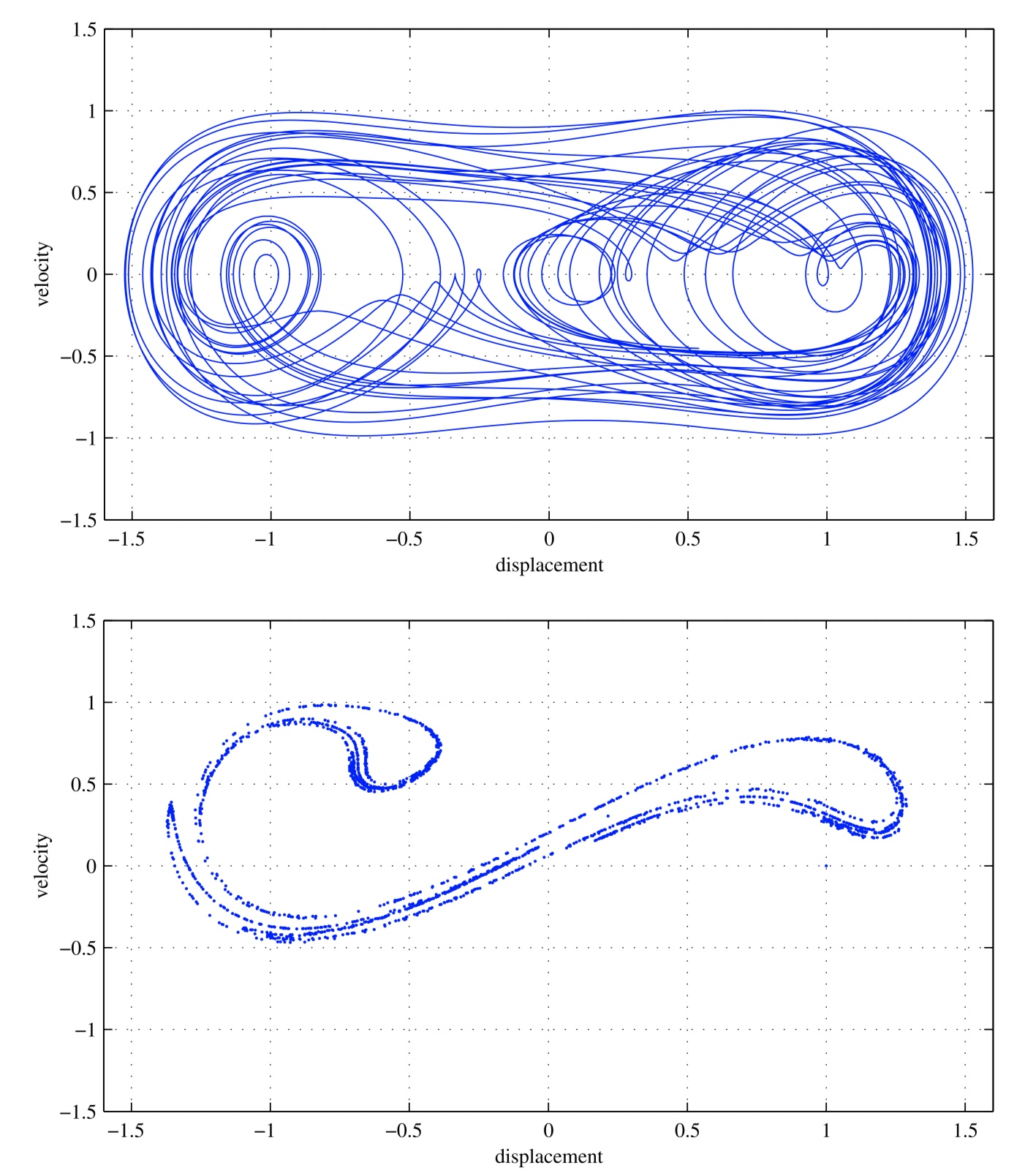Phase-space diagram of a chaotic Duffing oscillator
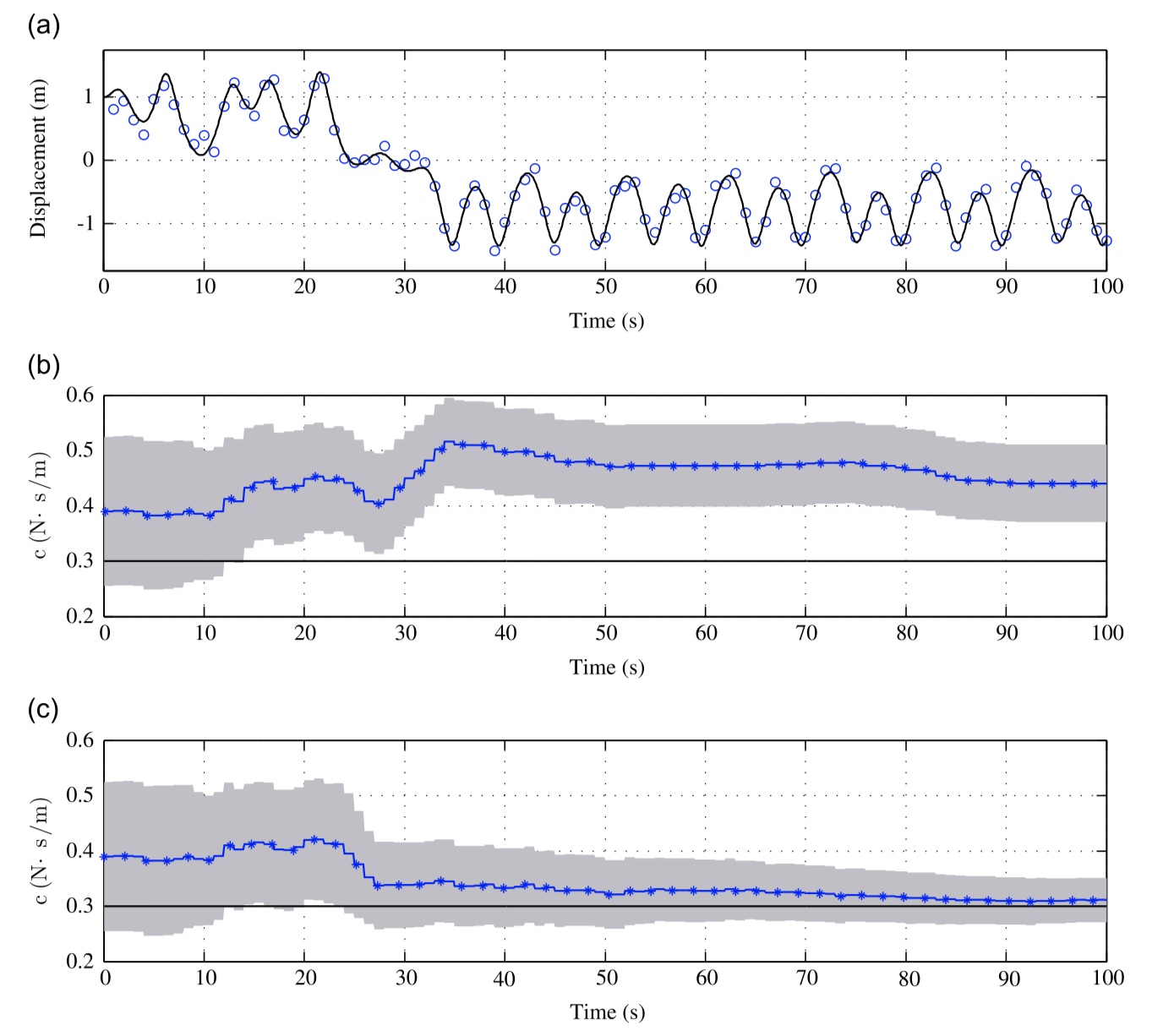Parameter estimates with sparse observational data of a Duffing oscillator
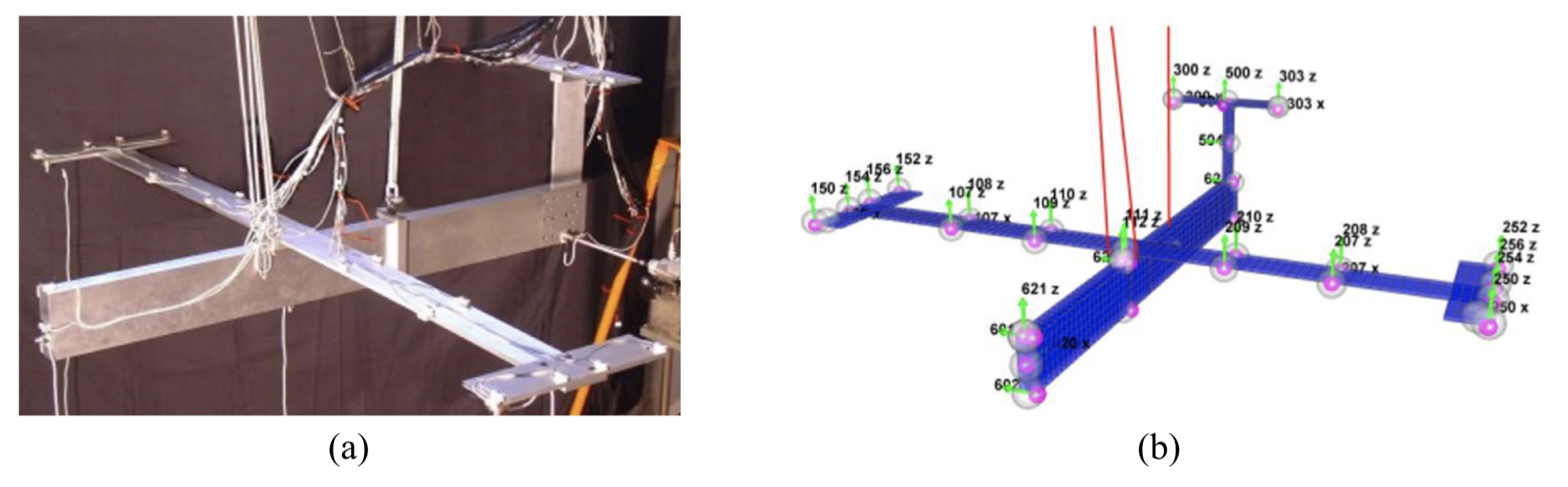AIRMOD (a) the physical structure and (b) the finite element model
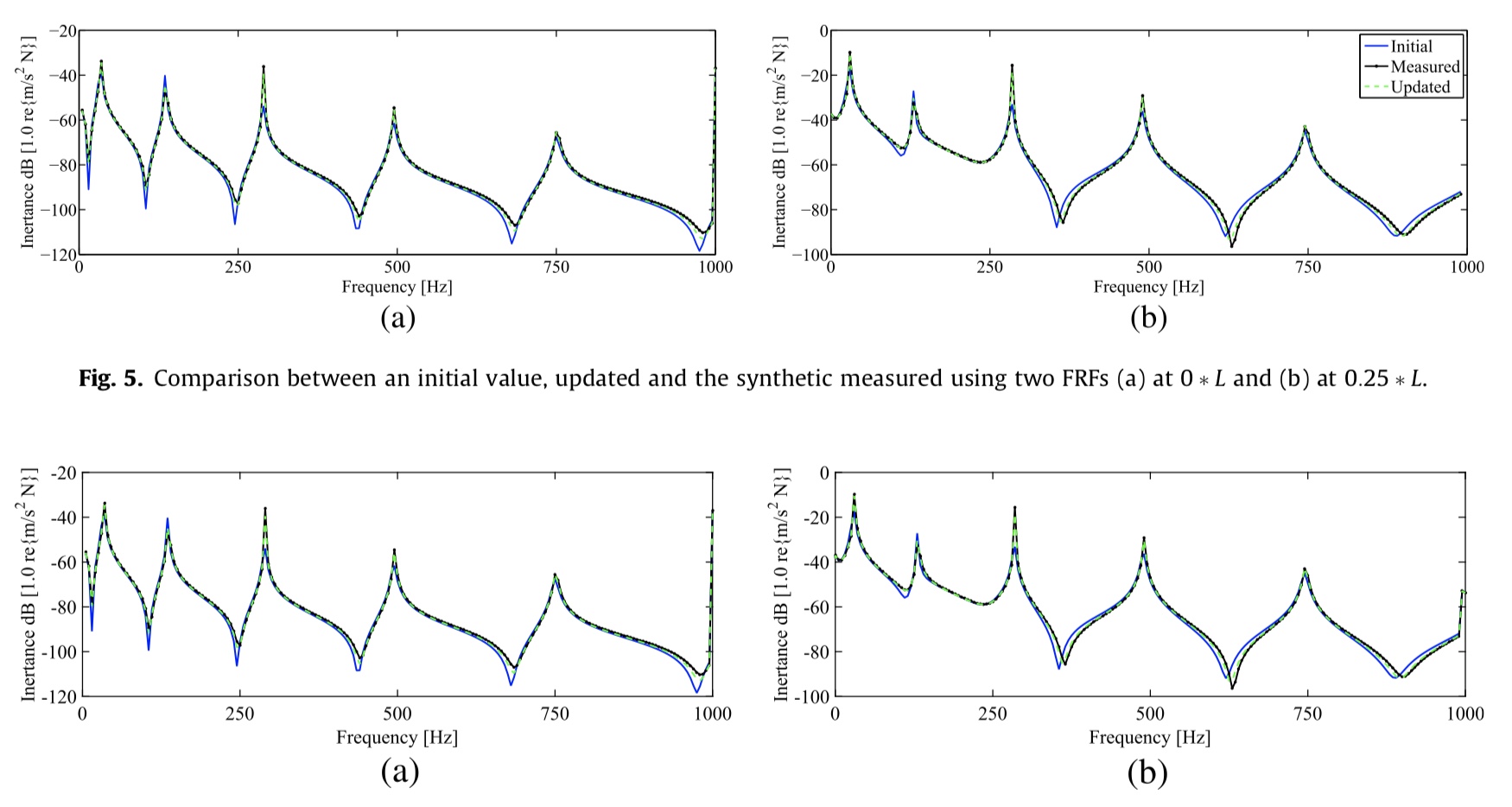Comparison between an initial value, updated and measured frequency response function of a dynamic system
An experimental system used in out study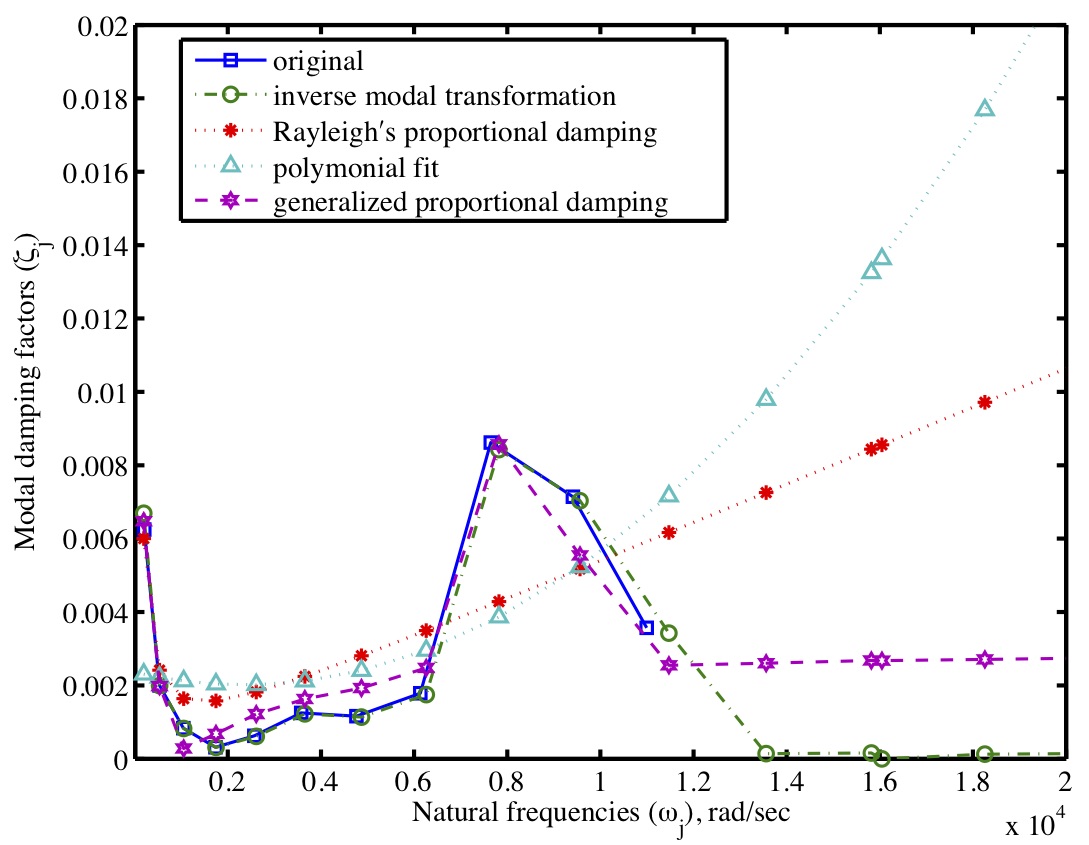
Fitting the modal damping matrix
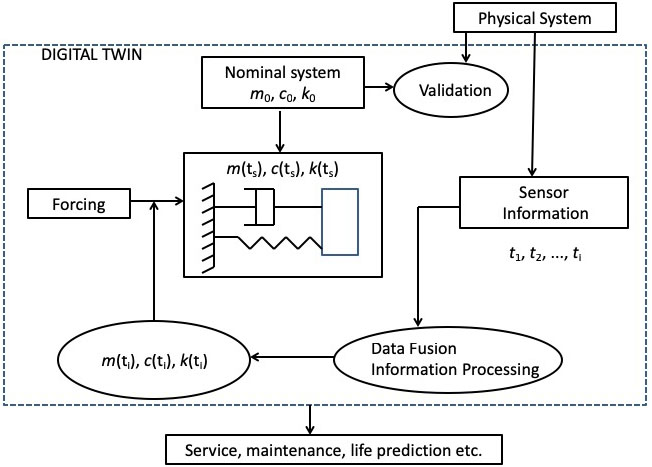The overview of constructing a digital twin for a single-degree-of-freedom dynamic system
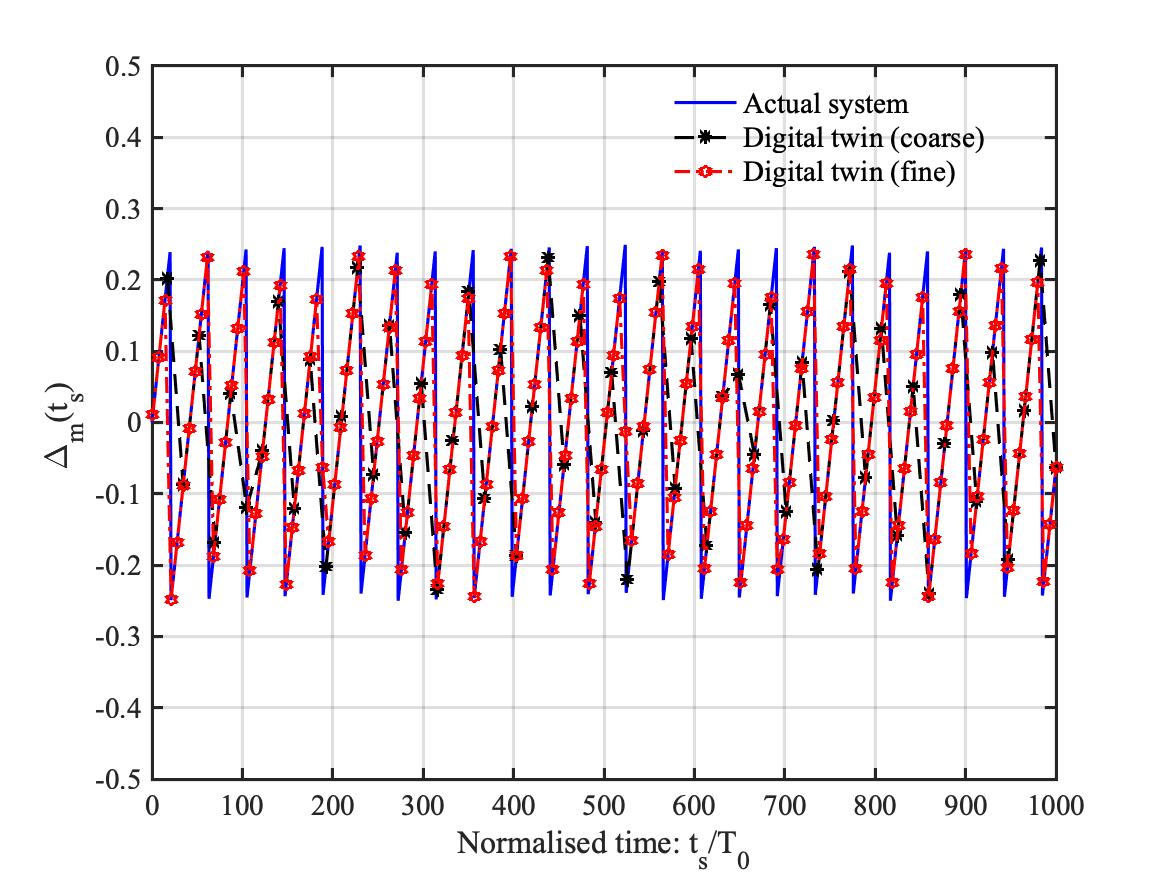Digital twin constructed with different slow-time sampling