Sondipon Adhikari

Professor Sondipon Adhikari (FRAeS)
Chair of Aerospace Engineering
College of Engineering, Swansea University
Bay Campus, Fabian Way, Crymlyn Burrows
Swansea, SA1 8EN, United Kingdom
Phone: + 44 (0)1792 602088, Fax: + 44 (0)1792 295676
Email: S.Adhikari@swansea.ac.uk, Sondipon.Adhikari@gmail.com
Twitter Linkedin

 
 
 
 
 
Dynamics of Complex Systems
A word-cloud from the title of the journal papers
Figure: A word-cloud from the title of the journal papers

Professor Adhikari's research works in this field contribute to the following sub areas: A brief description of the research topics and some key journal publications are given below.

B.1. Discrete damped systems

Numerical finite element models of complex dynamical systems can have millions of degrees of freedom. Efficient dynamic analysis of such complex system is of significant importance. Most conventional approaches ignore damping or use simplified models, often in an ad hoc manner. A focus of this research is to integrate advanced damping models with the dynamic analysis of multiple degrees-of-freedom systems. Viscous, nonviscous and non-proportional damping models are considered. Specifically, the following topics have been investigated:
  • Dynamic response and eigensolution analysis of non-viscously damped systems
  • Parametric sensitivity of eigenvalues and eigenvectors of damped dynamic systems
  • Properties of complex eigenvalues and eigenvectors of non-proportionally damped systems
  • Asymmetric non-conservative systems
  • Characterization of proportional damping
  • Mode veering in stressed structures
A typical result for parametric sensitivity analysis complex eigensolutions of a simple two degree-of-freedom system is shown below.
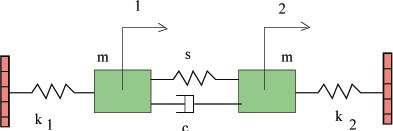A two degree-of-system damped system
A two degree-of-system damped system, m=1 Kg, k1 = 1000 N/m, c = 4 Ns/m
Imaginary part of [(d lambda_1)/dc]
Imaginary part of the first eigenvalue
Imaginary part of [(d lambda_2)/dc]
Imaginary part of the second eigenvalue
Book
Structural Dynamics with Generalized Damping Models: Analysis Adhikari, S., Structural Dynamics with Generalized Damping Models: Analysis, Wiley-ISTE, 2013 (Hardback 368 pp., ISBN: 9781848215214).
See the book in:

Key Journal Publications

  1. Batou, A. and Adhikari, S., “Optimal parameters of viscoelastic tuned-mass dampers,” Journal of Sound and Vibration, Vol. 445, No. 4, 2019, pp. 17–28.
  2. Khodaparast, H. H., Madinei, H., Friswell, M. I., Adhikari, S., Coggon, S., and Cooper, J., “An extended harmonic balance method based on incremental nonlinear control parameters,” Mechanical Systems and Signal Processing, Vol. 85, No. 2, 2017, pp. 716-729.
  3. Chakraborty, S., Chatterjee, T., Chowdhury, R., and Adhikari, S., “Robust design optimization for crashworthiness of vehicle side impact,” ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part B: Mechanical Engineering, Vol. 3, No. 3, 2017, pp. 031002:1-9.
  4. Chandrashaker, A., Adhikari, S., and Friswell, M. I., “Quantification of vibration localization in periodic structures,” ASME Journal of Vibration and Acoustics, Vol. 138, No. 2, 2016, pp. 021002:1-9.
  5. Dey, S., Mukhopadhyay, T., Adhikari, S., and Khodaparast, H. H., “A response surface modelling approach for resonance driven reliability based optimization of composite shells,” Periodica Polytechnica Civil Engineering, Vol. 60, No. 1, 2016, pp. 103-111.
  6. Beaverstock, C., Friswell, M. I., Adhikari, S., Richardson, T. S., and Du Bois, J. L., “Automatic mode tracking in flight mechanics using a spanning algorithm,” Aerospace Science and Technology, Vol. 47, No. 12, 2015, pp. 54-67.
  7. Dey, S., Sarkar, S., Karmakar, A., and Adhikari, S., “Effect of twist and rotation on vibration of functionally graded conical shells,” International Journal of Mechanics and Materials in Design, Vol. 11, No. 4, 2015, pp. 425-437.
  8. Mukhopadhyay, T., Chowdhury, R., Chakrabarti, A., and Adhikari, S., “Optimum design of FRP bridge deck: an efficient RS-HDMR based approach,” Structural and multidisciplinary optimization, Vol. 52, No. 3, 2015, pp. 459-477.
  9. Adhikari, S., Murmu, T., Gilchrist, D. J. E., and McCarthy, M. A., “Nonlocal normal modes for nanoscale dynamical systems,” Mechanical System and Signal Processing,Vol. 60-61, No. 8, 2015, pp. 583-603.
  10. Dey, S., Adhikari, S., and Karmakar, A., “Impact response of functionally graded conical shells,” Latin American Journal of Solids and Structures, Vol. 12, No. 1, 2015, pp. 133-152.
  11. Adhikari, S., “An iterative approach for nonproportionally damped systems,” Mechanics Research Communications, Vol. 38, No. 3, 2011, pp. 226-230.
  12. du Bois, J. L., Adhikari, S., and Lieven, N. A. J., “On the quantification of eigenvalue curve veering: A veering index,” Transactions of ASME, Journal of Applied Mechanics,Vol. 78, No. 4, 2011, pp. 041007:1-8.
  13. Kerfriden, P., Gosselet, P., Adhikari, S., and Bordas, S., “Bridging the proper orthogonal decomposition methods and augmented Newton-Krylov algorithms: An adaptive model order reduction for highly nonlinear mechanical problems,” Computer Methods in Applied Mechanics and Engineering, Vol. 200, No. 5-8, 2011, pp. 850-866.
  14. DiazDelaO, F. A. and Adhikari, S., “Structural dynamic analysis using Gaussian process emulators,” Engineering Computations, Vol. 27, No. 5, 2010, pp. 580-605.
  15. du Bois, J. L., Adhikari, S., and Lieven, N. A. J., “Mode veering in stressed framed structures,” Journal of Sound and Vibration, Vol. 322, No. 4-5, May 2009, pp. 1117-1124.
  16. Phani, S. A. and Adhikari, S., “Rayleigh quotient and dissipative systems,” Transactions of ASME, Journal of Applied Mechanics, Vol. 75, No. 6, November 2008, pp. 061005:1-6.
  17. Murugan, S., Flores, E. I. S., Adhikari, S., and Friswell, M. I., “Optimal design of variable fibre spacing composites for morphing aircraft skins,” Composite Structures,Vol. 94, No. 5, 2012, pp. 1626-1633.
  18. Ajaj, R. M., Friswell, M. I., Flores, E. I. S., Keane, A., Isikveren, A. T., Allegri, G., and Adhikari, S., “An integrated conceptual design study using span morphing technology,” Journal of Intelligent Material Systems and Structures, Vol. 25, No. 8, 2014, pp. 989-1008.
  19. Adhikari, S., “Damping modelling using generalized proportional damping,” Journal of Sound and Vibration, Vol. 293, No. 1-2, May 2006, pp. 156-170.
  20. Adhikari, S., “Optimal complex modes and an index of damping non-proportionality,” Mechanical System and Signal Processing, Vol. 18, No. 1, January 2004, pp. 1-27.
  21. Adhikari, S. and Friswell, M. I., “Authors’ reply to ‘Comments on Eigenderivative analysis of asymmetric non-conservative systems’,” International Journal of Numerical Methods in Engineering, Vol. 56, No. 2, 2003, pp. 329-330.
  22. Adhikari, S., “Classical normal modes in non-viscously damped linear systems,” AIAA Journal, Vol. 39, No. 5, May 2001, pp. 978-980.
  23. Adhikari, S. and Friswell, M. I., “Eigenderivative analysis of asymmetric non-conservative systems,” International Journal for Numerical Methods in Engineering,Vol. 51, No. 6, June 2001, pp. 709-733.
  24. Adhikari, S., “Calculation of derivative of complex modes using classical normal modes,” Computer and Structures, Vol. 77, No. 6, August 2000, pp. 625-633.
  25. Friswell, M. I. and Adhikari, S., “Derivatives of complex eigenvectors using Nelson's method,” AIAA Journal, Vol. 38, No. 12, December 2000, pp. 2355-2357.
  26. Adhikari, S., “Author’s Closure: ‘Comments on Modal Analysis of Linear Asymmetric Non-conservative Systems’ by D. L. Cronin,” ASCE Journal of Engineering Mechanics,Vol. 126, No. 12, December 2000, pp. 1307-1308.
  27. Adhikari, S., “On symmetrizable systems of second kind,” Transactions of ASME, Journal of Applied Mechanics, Vol. 67, No. 4, December 2000, pp. 797-802.
  28. Adhikari, S., “Rates of change of eigenvalues and eigenvectors in damped dynamic systems,” AIAA Journal, Vol. 37, No. 11, November 1999, pp. 1452-1458.
  29. Adhikari, S., “Modal analysis of linear asymmetric non-conservative systems,” ASCE Journal of Engineering Mechanics, Vol. 125, No. 12, December 1999, pp. 1372-1379.

B.2. Continuous systems

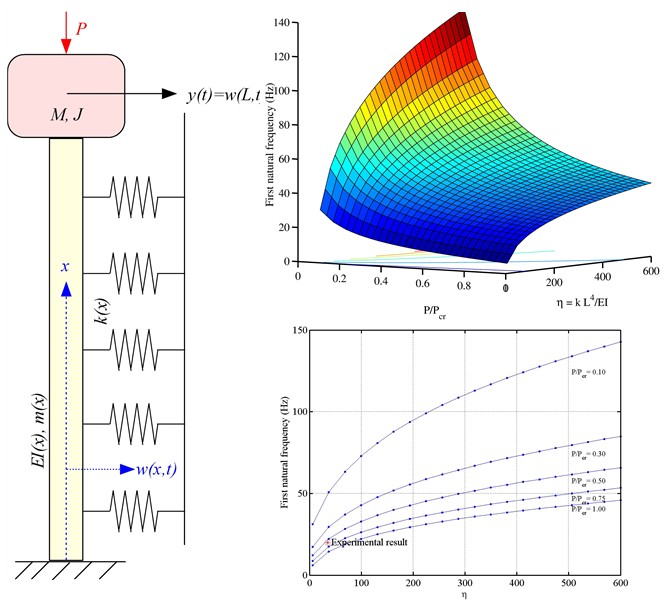
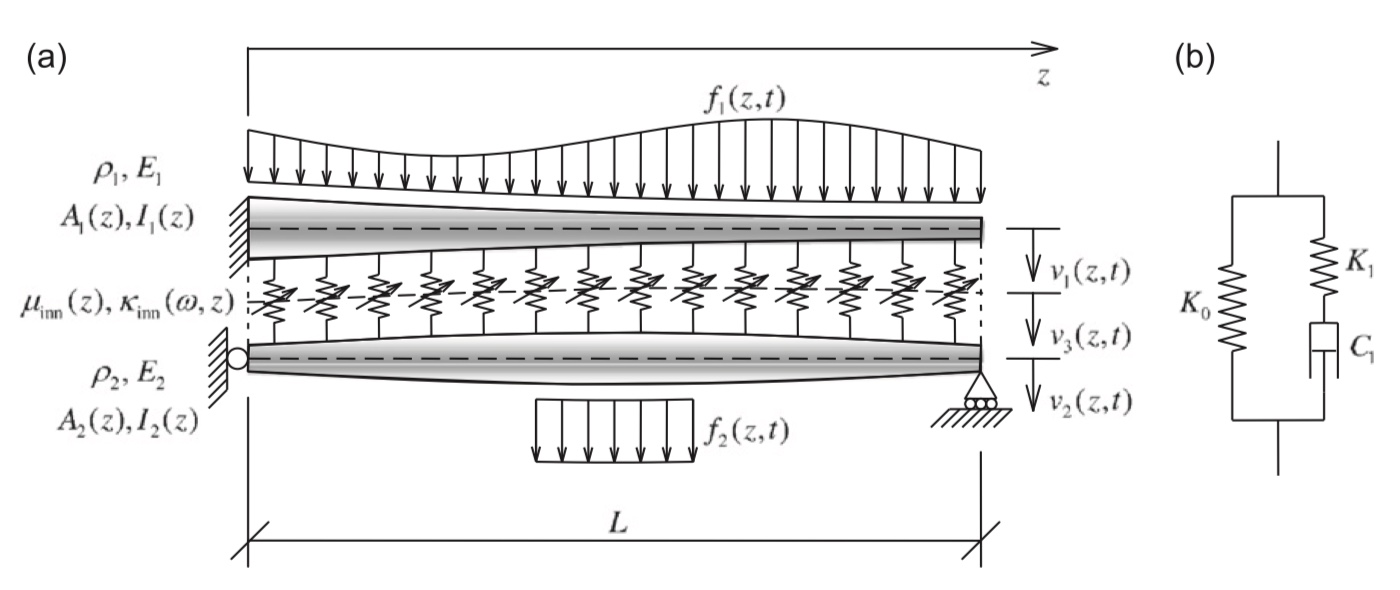
Most engineering dynamic systems are continuous systems, also known as distributed parameter systems. Example include aircraft wings, fuselage, bridges and rail tracks. When continuum models are used, the equation of motion is expressed by partial differential equations. Typically up-to fourth-order partial differential equations in one or two dimensions are employed. The advantage of using a continuum model, as opposed to using the more conventional discretised model (e.g., using a finite element approach), is that the continuum model and consequently the results are exact in nature. Therefore, they can be used to validate numerical results form discrete systems. A disadvantage of continuous systems for dynamic problems is that often exact closed-form solutions are difficult to obtain, In such cases, approximations need to be developed. Our work involves proposing new approximate solutions for continuous systems used to model important engineering structures such as wind turbine tower and piles in a soil medium.
Continuum model of a pile Continuum model of a pile in soil and its fundamental natural frequency Double viscoelastic beam model Double-beam dynamic system (a) the continuum model; (b0 rheological idealisation.

Key Journal Publications

  1. Machado, M. R., Adhikari, S., and Dos-Santos, J. M. C., “Spectral element method for a one-dimensional damaged structure with distributed random properties,” Journal of the Brazilian So- ciety of Mechanical Sciences and Engineering, Vol. 40, No. 8, 2018, pp. 415:1-16.
  2. Arany, L., Bhattacharya, S., Adhikari, S., Hogan, S. J., and Macdonald, J., “An analytical model to predict the natural frequency of offshore wind turbines on three-spring flexible foundations using two different beam models,” Soil Dynamics and Earthquake Engineering, Vol. 74, No. 1, 2015, pp. 40-45.
  3. Palmeri, A. and Adhikari, S., “A Galerkin-type state-space approach for transverse vibrations of slender double-beam systems with viscoelastic inner layer,” Journal of Sound and Vibration, Vol. 330, No. 26, 2011, pp. 6372-6386.
  4. Bhattacharya, S., Adhikari, S., and Alexander, N. A., “A simplified method for unified buckling and dynamic analysis of pile-supported structures in seismically liquefiable soils,” Soil Dynamics and Earthquake Engineering, Vol. 29, No. 8, August 2009, pp. 1220-1235.
  5. Adhikari, S. and Bhattacharya, S., “Dynamic instability of pile-supported structures in liquefiable soils during earthquakes,” Shock and Vibration, Vol. 15, No. 6, 2008, pp. 665-685.
  6. Bhattacharya, S., Dash, S. R., and Adhikari, S., “On the mechanics of failure of pile-supported structures in liquefiable deposits during earthquakes,” Current Science,Vol. 94, No. 5, 2008, pp. 605-611.
  7. Adhikari, S., Lei, Y., and Friswell, M. I., “Modal analysis of non-viscously damped beams,” Transactions of ASME, Journal of Applied Mechanics, Vol. 74, No. 5, September 2007, pp. 1026-1030.

B.3. Nonviscously damped discrete systems

The nature of damping forces is one of the least understood topics in structural dynamics. From the theory of classical mechanics, we know why the inertia and elastic forces are as they are, but the same is not exactly true for damping. Unlike the inertia and elastic forces, it is not clear what are the relevant state-variables that affect the damping forces. By far the most common approach is to assume so-called 'viscous damping', which supposes that the instantaneous generalized velocities are the only relevant state-variables that determine damping. However, viscous damping cannot be the only damping mechanism within the scope of linear analysis, examples are damping in composite materials, energy dissipation in structural joints, damping mechanism in composite beams, to mention only a few. This demands development of new methodologies to deal with non-viscously damped systems. This is the main focus of this research.

A key issue in considering non-viscously damped systems is to decide on an appropriate damping model. In principle, any causal model which makes the energy dissipation functional non-negative is a possible candidate for a damping model.

A representative selection of non-viscous damping functions in the Laplace domain Table: A representative selection of non-viscous damping functions in the Laplace domain
Possibly the most general way to model damping within the linear range is to use non-viscous damping models which depend on the past history of motion via convolution integrals over some kernel functions. The damping force using such a model can be expressed by
∫ t Fd(t) = G(t,τ)˙𝔲(τ)dτ -∞

where 𝔲(t) ∈ ℝN is the vector of generalized coordinates with t ∈ ℝ+ denotes time. The kernel functions or others closely related to them are described under many different names in the literature of different subjects: for example, retardation functions, heredity functions, after-effect functions, relaxation functions. In the special case when 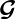G(t, τ) = Cδ(t - τ), where δ(t) is the Dirac-delta function, above equation, reduces to the case of viscous damping. The damping model of this kind is a further generalisation of the familiar viscous damping. The central theme of this research is to analyse multiple-degree-of-freedom linear systems whose damping characteristics may be successfully modelled by the above equation. It is assumed that the system is 'non-proportionally damped', that is, the equations of motion cannot be decoupled by the undamped eigenvectors. Several new computational methods and physical concepts have been developed.

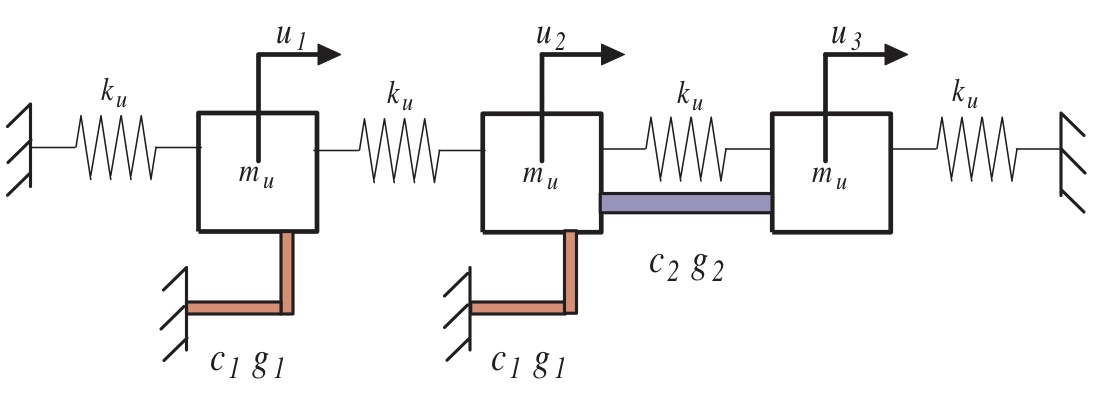Three-DOF system with nonviscous damping A three-DOF system with nonviscous damping 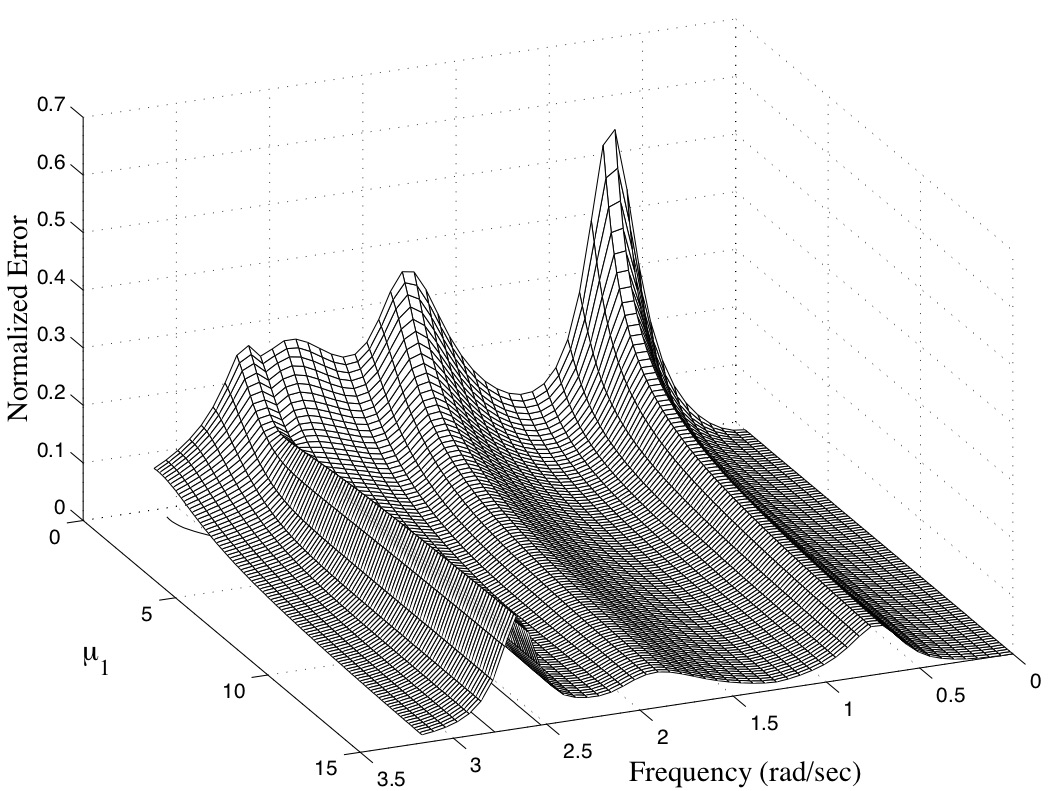Error in the transfer function Typical error in the norm of the transfer function matrix due to the viscous damping assumption

Key Journal Publications

  1. Adhikari, S. and Pascual, B., “Iterative methods for eigenvalues of viscoelastic systems,” Transactions of ASME, Journal of Vibration and Acoustics, Vol. 133, No. 2, April 2011, pp. 021002:1-7.
  2. Friswell, M. I., Dutt, J. K., Adhikari, S., and Lees, A. W., “Time domain analysis of a viscoelastic rotor using internal variable models,” International Journal of Mechanical Sciences, Vol. 52, No. 10, 2010, pp. 1319-1324.
  3. Adhikari, S., “A general derivation of dynamic response of viscoelastic structures,” International Journal of Aerospace Innovations, Vol. 2, No. 1-2, 2010, pp. 29-41.
  4. Adhikari, S., “A reduced second-order approach for linear viscoelastic oscillators,” Transactions of ASME, Journal of Applied Mechanics, Vol. 77, No. 4, July 2010, pp. 041003:1-8.
  5. Adhikari, S. and Pascual, B., “Eigenvalues of linear viscoelastic systems,” Journal of Sound and Vibration, Vol. 325, No. 4-5, September 2009, pp. 1000-1011.
  6. Sieber, J., Wagg, D. J., and Adhikari, S., “On the interaction of exponential non-viscous damping with symmetric nonlinearities,” Journal of Sound and Vibration,Vol. 314, No. 1-2, 2008, pp. 1-11.
  7. Adhikari, S., “Dynamic response characteristics of a non-viscously damped oscillator,” Transactions of ASME, Journal of Applied Mechanics, Vol. 75, No. 1, January 2008, pp. 011003:1-12.
  8. Adhikari, S. and Friswell, M. I., “The calculation of eigensolution derivatives for non-viscously damped systems using Nelson’s method,” AIAA Journal, Vol. 44, No. 8, August 2006, pp. 1799-1806.
  9. Adhikari, S., “Qualitative dynamic characteristics of a non-viscously damped oscillator,” Proceedings of the Royal Society of London, Series- A, Vol. 461, No. 2059, July 2005, pp. 2269-2288.
  10. Adhikari, S. and Wagner, N., “Direct time-domain approach for exponentially damped systems,” Computer and Structures, Vol. 82, No. 29-30, November 2004, pp. 2453-2461.
  11. Adhikari, S. and Woodhouse, J., “Quantification of non-viscous damping in discrete linear systems,” Journal of Sound and Vibration, Vol. 260, No. 3, February 2003, pp. 499-518.
  12. Wagner, N. and Adhikari, S., “Symmetric state-space formulation for a class of non-viscously damped systems,” AIAA Journal, Vol. 41, No. 5, 2003, pp. 951-956.
  13. Adhikari, S. and Wagner, N., “Analysis of asymmetric non-viscously damped linear dynamic systems,” Transactions of ASME, Journal of Applied Mechanics, Vol. 70, No. 6, December 2003, pp. 885-893.
  14. Adhikari, S., “Dynamics of non-viscously damped linear systems,” ASCE Journal of Engineering Mechanics, Vol. 128, No. 3, March 2002, pp. 328-339.
  15. Adhikari, S., “Derivative of eigensolutions of non-viscously damped linear systems,” AIAA Journal, Vol. 40, No. 10, October 2002, pp. 2061-2069.
  16. Adhikari, S., “Eigenrelations for non-viscously damped systems,” AIAA Journal,Vol. 39, No. 8, August 2001, pp. 1624-1630.

B.4. Nonlocal damped continuous systems

Dynamic analysis of distributed systems with non-local elasticity and nonviscous damping is considered. A fundamental difference here compared to the previous cases is that here we get integro-partial differential equations. For certain choices of the kernel function, an integro-partial differential equation may be transformed into an easier differential form. But this is general, not true. Our research considers both the cases. Completely new type of finite element methods has been developed to consider such equations for one-dimensional systems (beams, rods). Future research is needed for higher dimensional systems (2D and 3D problems). Our current results give efficient ways to obtain natural frequencies, mode shapes and dynamic response of nonlocal damped continuous systems. A unique feature of these studies is that advanced damping models have been considered, which is often ignored.
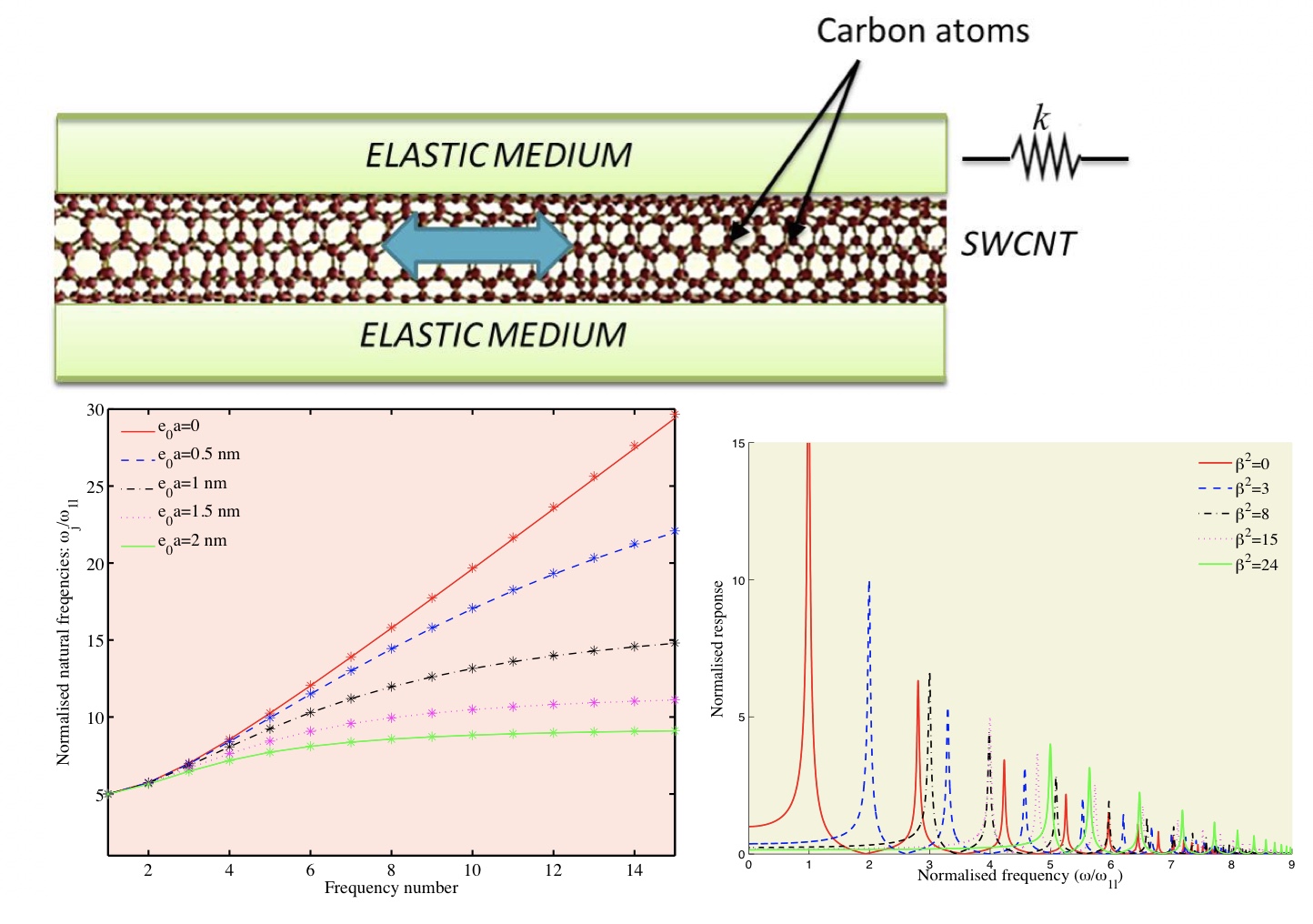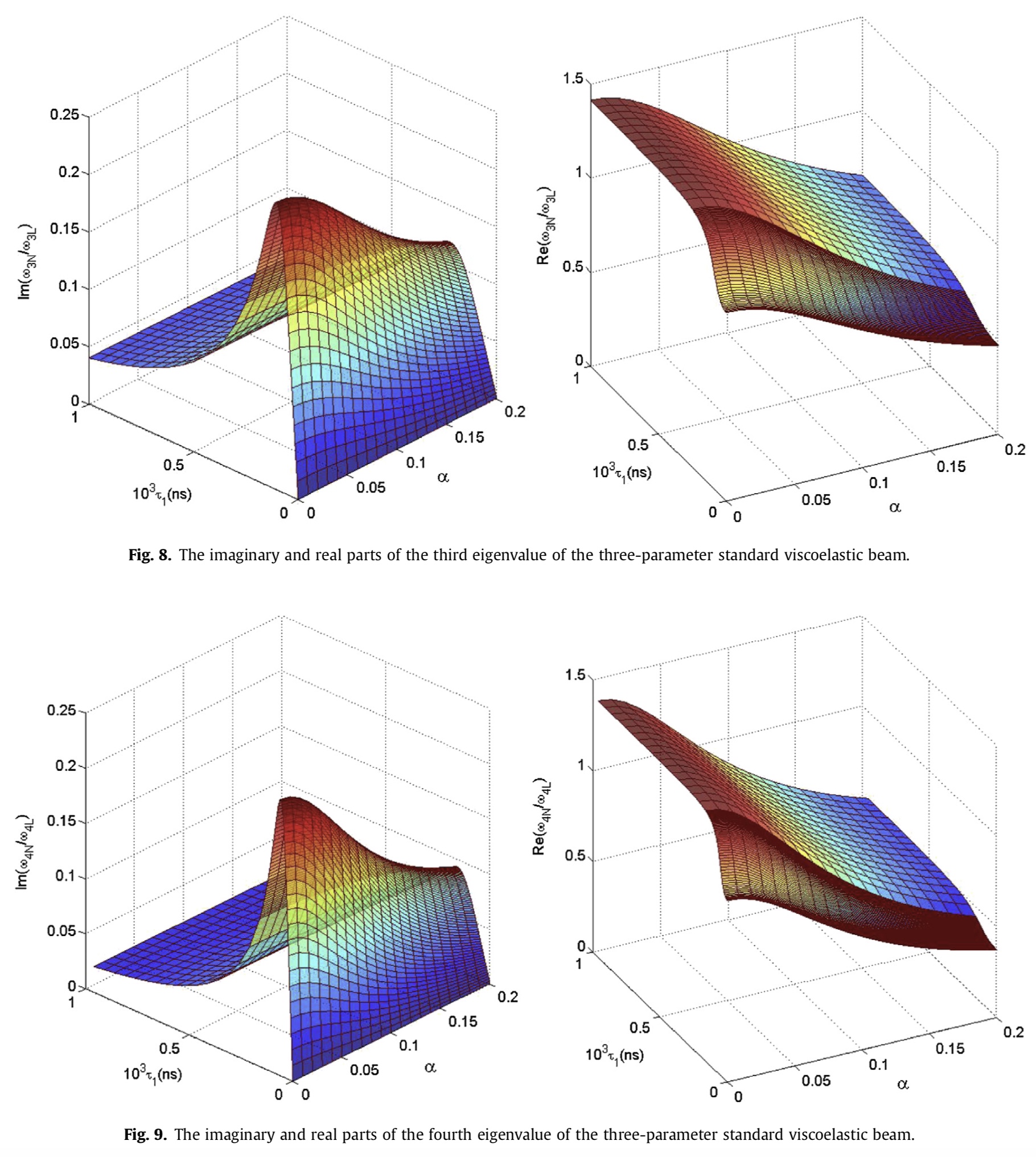Damped viscoelastic nonlocal Euler-Bernoulli beam model A damped viscoelastic nonlocal Euler-Bernoulli beam model Fullerene frequency The third eigenvalue of a three-parameter standard viscoelastic beam.

Key Journal Publications

  1. Karlicic, D., Cajic, M., and Adhikari, S., “Dynamic stability of a nonlinear multiple-nanobeam systems,” Nonlinear Dynamics, Vol. 93, No. 4, 2018, pp. 1495-1517.
  2. Lei, Y., Murmu, T., Adhikari, S., and Friswell, M. I., “Asymptotic frequencies of various damped nonlocal beams and plates,” Mechanics Research Communication,Vol. 62, No. 1, 2014, pp. 94-101.
  3. Adhikari, S., Murmu, T., and McCarthy, M., “Frequency domain analysis of nonlocal rods embedded in an elastic medium,” Physica E: Low-dimensional Systems and Nanostructures, Vol. 59, No. 5, 2014, pp. 33-40.
  4. Lei, Y., Murmu, T., Adhikari, S., and Friswell, M. I., “Dynamic characteristics of damped viscoelastic nonlocal Euler-Bernoulli beams,” European Journal of Mechanics - A/Solids, Vol. 42, No. 12, 2013, pp. 125-136.
  5. Lei, Y., Friswell, M. I., and Adhikari, S., “Vibration of nonlocal Kelvin-Voigt viscoelastic damped Timoshenko beams,” International Journal of Engineering Science,Vol. 66-67, No. 1, 2013, pp. 1-13.
  6. Adhikari, S., Murmu, T., and McCarthy, M., “Dynamic finite element analysis of axially vibrating nonlocal rods,” Finite Elements in Analysis and Design, Vol. 63, No. 1, 2013, pp. 42-50.
  7. Friswell, M. I., Adhikari, S., and Lei, Y., “Nonlocal finite element analysis of damped beams,” International Journal of Solids and Structures, Vol. 44, No. 22-23, November 2007, pp. 7564-7576.
  8. Friswell, M. I., Adhikari, S., and Lei, Y., “Vibration analysis of beams with non-local foundations using the finite element method,” International Journal for Numerical Methods in Engineering, Vol. 71, No. 11, September 2007, pp. 1365-1386.
  9. Lei, Y., Friswell, M. I., and Adhikari, S., “A Galerkin method for distributed systems with non-local damping,” International Journal of Solids and Structures, Vol. 43, No. 11-12, 2006, pp. 3381-3400.

Home | Research | Publications | Teaching | Lectures | Students and Post-docs | Education & awards | Professional activities | Contact | Departmental web page | Downloads