
Figure: A word-cloud from the title of the journal papers
Professor Adhikari's research works in this field contribute to the following sub areas:
A brief description of the research topics and some key journal publications are given below.
A.1. Mechanics of metamaterials
Mechanical metamaterials have surged to the forefront over the past five years against the backdrop of the unprecedented developments in optical, electromagnetic and acoustic metamaterials. Metamaterials are designer media with periodic units comprised of unique tailor-made geometry (see the Figure below) and patterns that produce extraordinary and unusual bulk properties not seen in conventional materials. The global metamaterials market is expected to reach $60 billion by 2025 with an expected compound annual growth rate of 25% from 2018 to 2026.
 Three main types of mechanical metamaterials Three main types of mechanical metamaterials |
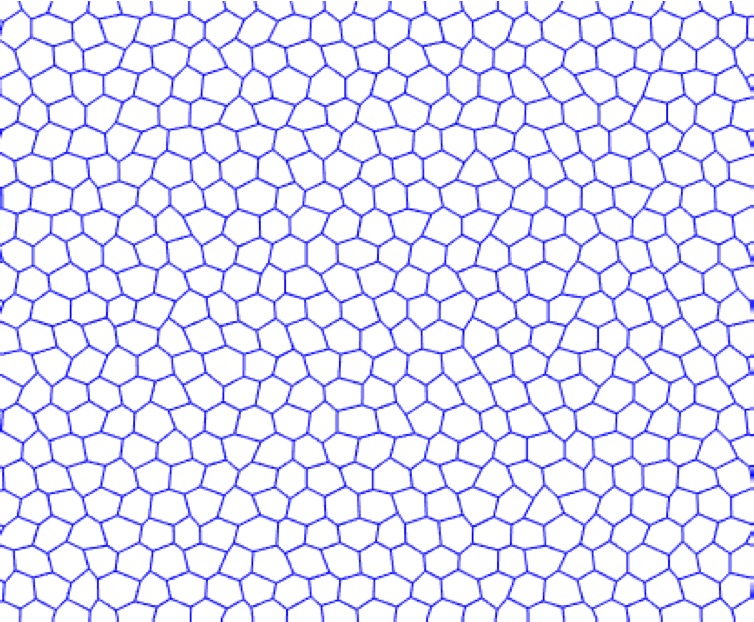 An example of a disordered cellular metamaterial (hexagonal unit cells) An example of a disordered cellular metamaterial (hexagonal unit cells) |
The effective properties of metamaterials originate from the geometry and structure, and not from the intrinsic property of the constitutive material. Intense research in recent years shows truly exciting developments such as ultralight metamaterials approaching theoretical strength limit, pentamode materials, negative refraction elastic waves, elastic cloaking and hyperbolic elastic metamaterials. Our research focuses on the effect of three pivotal issues, namely random disorder, damping and nonlinearity in mechanical metamaterials.
Key Journal Publications
- Mukhopadhyay, T., Adhikari, S., and Alu, A., “Theoretical limits for negative elastic moduli in subacoustic lattice materials,” Physical Review B, Vol. 99, No. 9, 2019, pp. 094108..
- Mukhopadhyay, T., Adhikari, S., and Alu, A., “Probing the
frequency-dependent elastic moduli of lattice materials,” Acta
Materialia, Vol. 165, No. 2, 2019, pp. 654-665.
- Mukhopadhyay, T., Adhikari, S., and Batou, A., “Viscoelastic mechanical properties of irregular quasi-periodic lattices with spatially correlated material and structural attributes,” International Journal of Mechanical Science, Vol. 150, No. 1, 2019, pp. 784–806.
- Mukhopadhyay, T., Mahata, T., Adhikari, S., and Zaeem, M. A., “Probing the shear modulus of two-dimensional multiplanar nanostructures and heterostructures,” Nanoscale, Vol. 10, No. 11, 2018, pp. 5280–5294..
- Mukhopadhyay, T., Mahata, T., Zaeem, M. A., and Adhikari, S., “Effective mechanical properties of multilayer nano-heterostructures,” Nature Scientific Reports, Vol. 7, No. 1, 2017, pp. 15818:1-13.
- Mukhopadhyay, T. and Adhikari, S., “Effective in-plane elastic properties of quasi-random spatially irregular hexagonal lattices,” International Journal of Engineering Science, Vol. 119, No. 10, 2017, pp. 142-179.
- Martinez-Ayuso, G., Friswell, M. I., Adhikari, S., Khodaparast, H. H., and Berger, H., “Homogenization of porous piezoelectrical materials,” International Journal of Solid and Structures, Vol. 113-114, No. 5, 2017, pp. 218-229.
- Mukhopadhyay, T., Mahata, T., Zaeem, M. A., and Adhikari, S., “Effective elastic properties of two dimensional multiplanar hexagonal nano-structures,” 2D Materials,Vol. 4, No. 2, 2017, pp. 025006:1-15.
- Mukhopadhyay, T. and Adhikari, S., “Stochastic mechanics of metamaterials,” Composite Structures, Vol. 162, No. 3, 2017, pp. 85-97.
- Mukhopadhyay, T. and Adhikari, S., “Effective in-plane elastic properties of auxetic honeycombs with spatial irregularity,” Mechanics of Materials, Vol. 95, No. 2, 2016, pp. 204-222.
- Mukhopadhyay, T. and Adhikari, S., “Equivalent in-plane elastic properties of irregular honeycombs: An analytical approach,” International Journal of Solids and Structures,Vol. 91, No. 8, 2016, pp. 169-184.
- Mukhopadhyay, T. and Adhikari, S., “Free vibration of sandwich panels with randomly irregular honeycomb core,” ASCE Journal of Engineering Mechanics, Vol. 141, No. 6, 2016, pp. 06016008:1-5.
A.2. Dynamics of nonlocal continuous systems
Nanoscale experiments demonstrate that the mechanical properties of nano-dimensional materials are much influenced by 'size effects' or 'scale effects'. The nonlocal elasticity theory (nonlocal mechanics) has emerged as one widely promising size-dependant continuum theory. Significant progress has been made in fundamental and applied computational research in this area. The robust conventional local elasticity theory underpins the bulk of application of continuum mechanics in applied science and engineering since its inception in the early nineteenth century. The utilisation of the local elasticity theory in the context of nanoscale objects (such as carbon nanotube and graphene structures, etc.) has been questioned repeatedly in various research articles over the past decade. Nonlocal elasticity theory, pioneered from the 1970s, can be applied over all scales and is considered to be more suitable for analysing popular nanoscale objects such as carbon nanotube and graphene sheets. Our research covers nonlocal elasticity theory for static, dynamic and stability analysis of wide-ranging nanostructures. These include nonlocal Euler-Bernoulli beams, nonlocal Timoshenko beams, nonlocal plates and coupled systems.
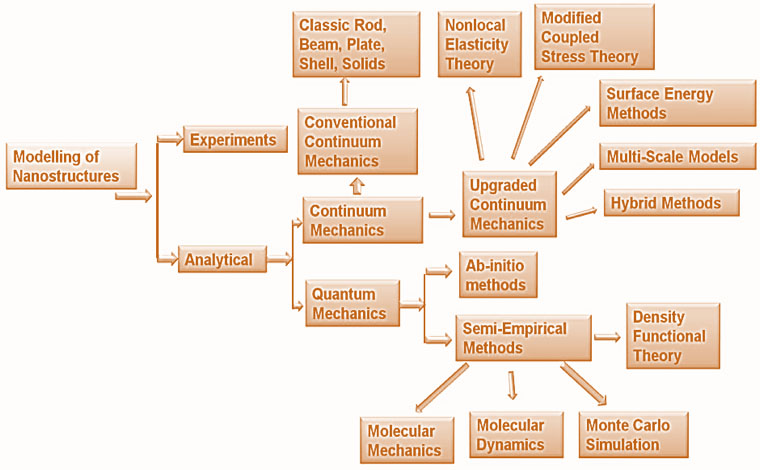 General approaches employed to model and study nanostructures General approaches employed to model and study nanostructures |
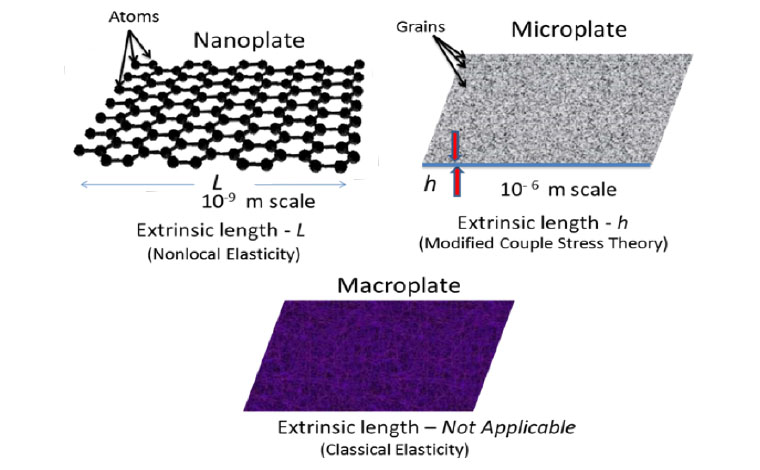 Extrinsic lengths in the plates of different scale Extrinsic lengths in the plates of different scale |
Book
 |
Karlicic, D. Murmu, T., Adhikari, S. and McCarthy, M., Non-local Structural Mechanics, Wiley-ISTE, 2015 (Hardback 354 pp., ISBN: 1848215223)
See the book in:
|
Key Journal Publications
- Zhang, D. P., Lei, Y., a and Adhikari, S., “Flexoelectric effect on vibration responses of piezoelectric nanobeams embedded in viscoelastic medium based on nonlocal elasticity theory,” Acta Mechanica, Vol. 229, No. 6, 2018, pp. 2379–2392.
- Karlicic, D., Kozic, P., Murmu, T., and Adhikari, S., “Vibration insight of a nonlocal viscoelastic coupled multi-nanorod system,” European Journal of Mechanics - A/Solids,Vol. 55, No. 12, 2015, pp. 132-145.
- Karlicic, D., Adhikari, S., Murmu, T., and Cajic, M., “Exact closed-form solution for non-local vibration and biaxial buckling of bonded multi-nanoplate system,” Composites Part B, Vol. 66, No. 2, 2014, pp. 328-339.
- Karlicic, D., Cajic, M., Murmu, T., and Adhikari, S., “Nonlocal longitudinal vibration of viscoelastically coupled double-nanorod systems,” European Journal of Mechanics - A/Solids, Vol. 49, No. 1, 2015, pp. 183-196.
- Murmu, T., Adhikari, S., McCarthy, M., and Wang, C. Y., “Insights into relative lower frequencies and buckling loads of monolayer graphene sheets via nonlocal elasticity theory: Size-dependent Young’s modulus approach,” Nanoscience and Nanotechnology Letters,Vol. 5, No. 10, 2013, pp. 1097-1102.
- Allegri, G., Scarpa, F., Chowdhury, R., and Adhikari, S., “Wave propagation in periodically supported nanoribbons: a nonlocal elasticity approach,” Transactions of ASME, Journal of Vibration and Acoustics, Vol. 135, No. 4, 2013, pp. 041017:1-8.
- Murmu, T. and Adhikari, S., “Nonlocal elasticity based vibration of initially pre-stressed coupled nanobeam systems,” European Journal of Mechanics - A/Solids,Vol. 34, No. 1, 2012, pp. 52-62.
- Murmu, T. and Adhikari, S., “Nonlocal vibration of bonded double-nanoplate-systems,” Composites Part B: Engineering, Vol. 42, No. 7, 2011, pp. 1901-1911.
- Murmu, T. and Adhikari, S., “Torsional vibration of carbon nanotube-buckyball systems based on nonlocal elasticity theory,” Physica E: Low-dimensional Systems and Nanostructures, Vol. 43, No. 6, 2011, pp. 1276-1280.
- Wang, C. W., Murmu, T., and Adhikari, S., “Mechanisms of nonlocal effect on the vibration of nanoplates,” Applied Physics Letters, Vol. 98, No. 15, 2011, pp. 153101:1-3.
- Murmu, T. and Adhikari, S., “Nonlocal vibration of carbon nanotubes with attached buckyballs at tip,” Mechanics Research Communications, Vol. 38, No. 1, 2011, pp. 62-67.
- Murmu, T. and Adhikari, S., “Axial instability of double-nanobeam-systems,” Physics Letters A, Vol. 375, No. 3, 2011, pp. 601-608.
- Murmu, T. and Adhikari, S., “Scale-dependent vibration analysis of prestressed carbon nanotubes undergoing rotation,” Journal of Applied Physics, Vol. 108, No. 12, 2010, pp. 123507:1-7.
- Murmu, T. and Adhikari, S., “Nonlocal effects in the longitudinal vibration of double-nanorod systems,” Physica E: Low-dimensional Systems and Nanostructures,Vol. 43, No. 1, 2010, pp. 415-422.
- Murmu, T. and Adhikari, S., “Nonlocal transverse vibration of double-nanobeam-systems,” Journal of Applied Physics, Vol. 108, No. 8, 2010, pp. 083514:1-9.
A.3. Nonlocal magneto-elasto dynamics
Magnetic field effects in nanotubes and nanoplates (graphene) are important for exciting potential applications in nanotechnology such as in nanoelectromechanical systems (NEMS), microelectromechanical systems (MEMS), nanosensors, spintronics, and nanocomposites. In recent years, research interest has grown on studying the magnetic properties of nanotubes and behaviour of nanotubes within a magnetic field. We have investigated the influence of a perpendicular magnetic field on the transport properties of carbon nanotubes (CNTs). The effects of an external magnetic field on the magnetic properties of nanotubes and nanowires were investigated. Research in this area involves multiscale and multiphysics concepts.
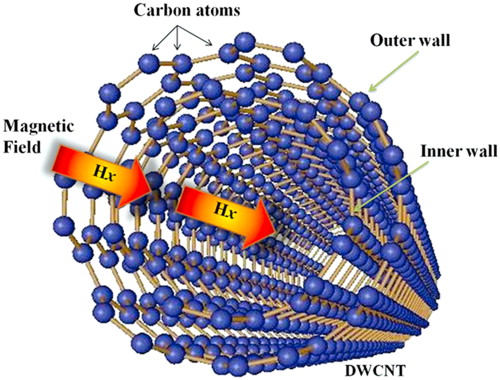 Armchair double-walled carbon nanotube subjected to axial magnetic field Armchair double-walled carbon nanotube subjected to axial magnetic field |
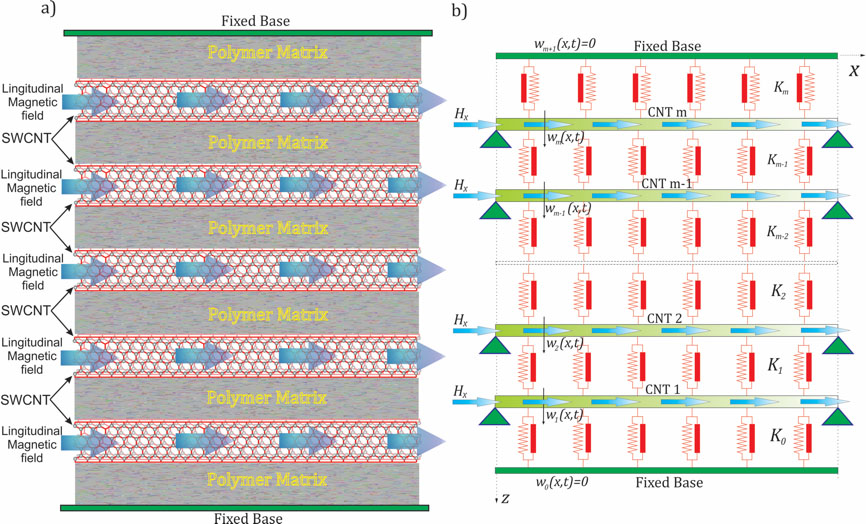 Axial magnetic field exerted on multiple SWCNTs embedded in polymer matrix Axial magnetic field exerted on multiple SWCNTs embedded in polymer matrix |
Key Journal Publications
- Karlicic, D., Cajic, M., Adhikari, S., Kozic, P., and Murmu, T., “Vibrating nonlocal multi-nanoplate system under inplane magnetic field,” European Journal of Mechanics - A/Solids, Vol. 64, No. 7-8, 2017, pp. 29-45.
- Mukhopadhyay, T., Mahata, A., Dey, S., and Adhikari, S., “Probabilistic analysis and design of {HCP} nanowires: An efficient surrogate based molecular dynamics simulation approach,” Journal of Materials Science & Technology, Vol. 32, No. 12, 2016, pp. 1345–1351.
- Karlicic, D., Cajic, M., Murmu, T., Kozic, P., and Adhikari, S., “Nonlocal longitudinal vibration of a complex multi-nanorod system affected by transversal magnetic field,” Meccanica, Vol. 50, No. 6, 2015, pp. 1605-1621.
- Ghavanloo, E., Fazelzadeh, S., Murmu, T., and Adhikari, S., “Radial breathing-mode frequency of elastically confined spherical nanoparticles subjected to circumferential magnetic field,” Physica E: Low-dimensional Systems and Nanostructures, Vol. 66, No. 2, 2015, pp. 228-233.
- Karlicic, D., Cajic, M., Murmu, T., and Adhikari, S., “Dynamics of multiple viscoelastic carbon nanotube based nanocomposites with axial magnetic field,” Journal of Applied Physics, Vol. 115, No. 23, 2014, pp. 234303:1-14.
- Murmu, T., Adhikari, S., and McCarthy, M., “Axial vibration of embedded nanorods under transverse magnetic field effects via nonlocal elastic continuum theory,” Journal of Computational and Theoretical Nanoscience, Vol. 11, No. 5, 2014, pp. 1230-1236.
- Murmu, T., McCarthy, M., and Adhikari, S., “In-plane magnetic field affected transverse vibration of embedded single-layer graphene sheets using equivalent nonlocal elasticity approach,” Composite Structures, Vol. 96, No. 2, 2013, pp. 57-63.
- Murmu, T., Adhikari, S., and McCarthy, M., “Vibration response of double-walled carbon nanotubes subjected to an externally applied longitudinal magnetic field: A nonlocal elasticity approach,” Journal of Sound and Vibration, Vol. 331, No. 23, 2012, pp. 5069-5086.
- Murmu, T., McCarthy, M., and Adhikari, S., “Nonlocal elasticity based magnetic field affected vibration response of double single-walled carbon nanotube systems,” Journal of Applied Physics, Vol. 111, No. 11, 2012, pp. 113511:1-7.
A.4 Atomistic computational method - Finite element / Molecular mechanics
The aim of this research is to develop efficient computational methods for nano-scale methods. The extension of well-established methods for the macro-scale systems to bio and nanosystems such as nanotubes, graphene sheets, DNA and proteins poses some significant challenges. These include: (a) the models describing bio and nanosystems can be very complex, computationally intensive and nonlinear, (b) the validation and calibration of the models are difficult due to the lack of enough high-quality experimental data across different length and time scales, and (c) there is a large amount of uncertainty in both the model and data. Over the past two decades, multi-scale methods have been developed to address the first two issues. Our approach includes (a) development of novel atomistic citrine element method based considering atomic binds in nanostructures as equivalent beams, (b) applying molecular mechanics approach to newly discovered nanostructures (e.g., carbon, Boron Nitride (BN), ZnO nanotubes and BN and Graphene sheets). In particular, we have investigated these issues:
- Elastic modulus of Graphene sheets and CNTs
- The role of Poisson's ratio in the structural model of CNTs and Graphene sheets
- Finite Element method and Molecular dynamic simulation of CNTS: analysis eigenvalues, eigenvectors, buckling loads and natural frequencies
- Mechanics and dynamics of non-homogenous structures such as DNA molecules, fullerenes, ZnO, BN
- Multiscale methods for CNT and Graphene composites
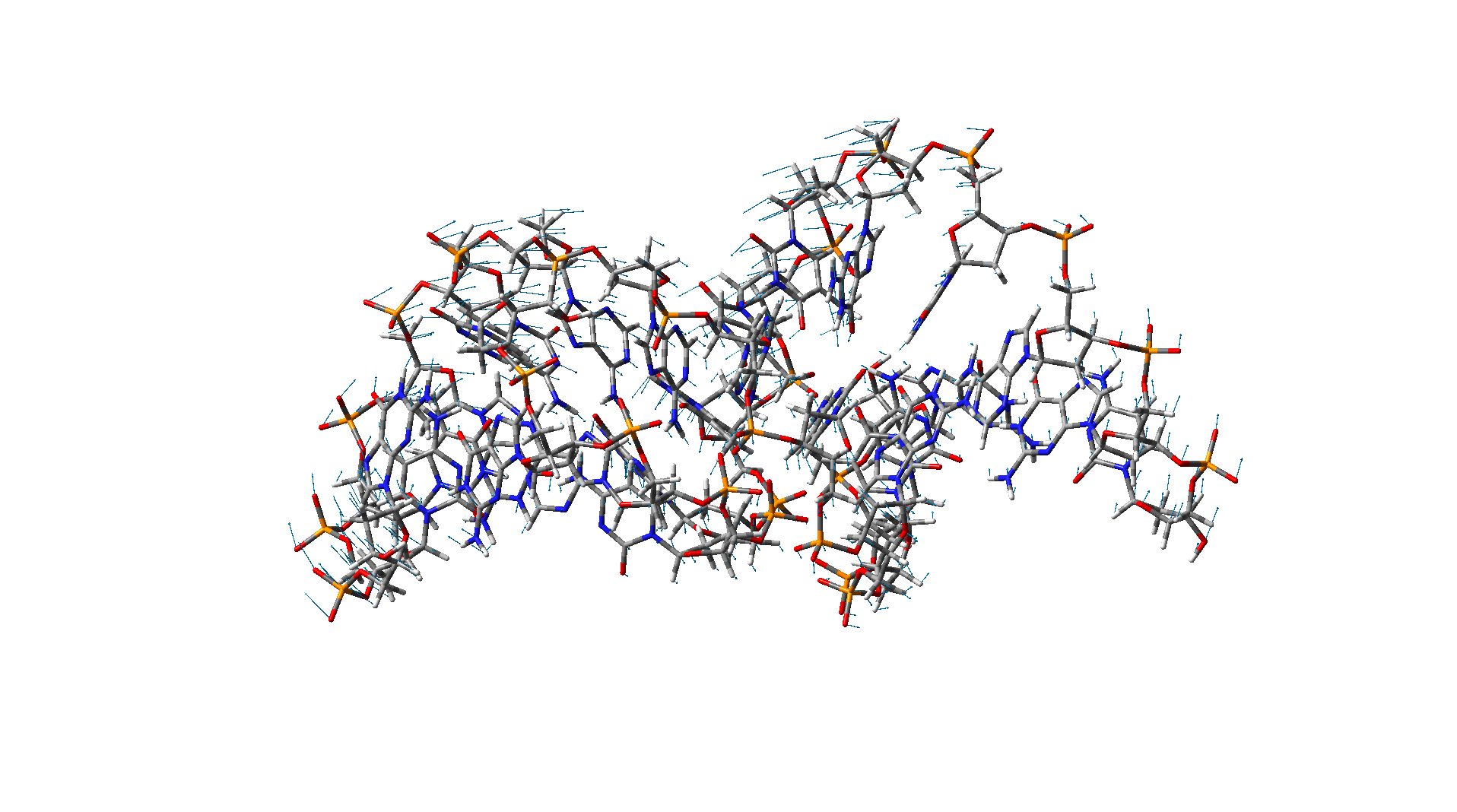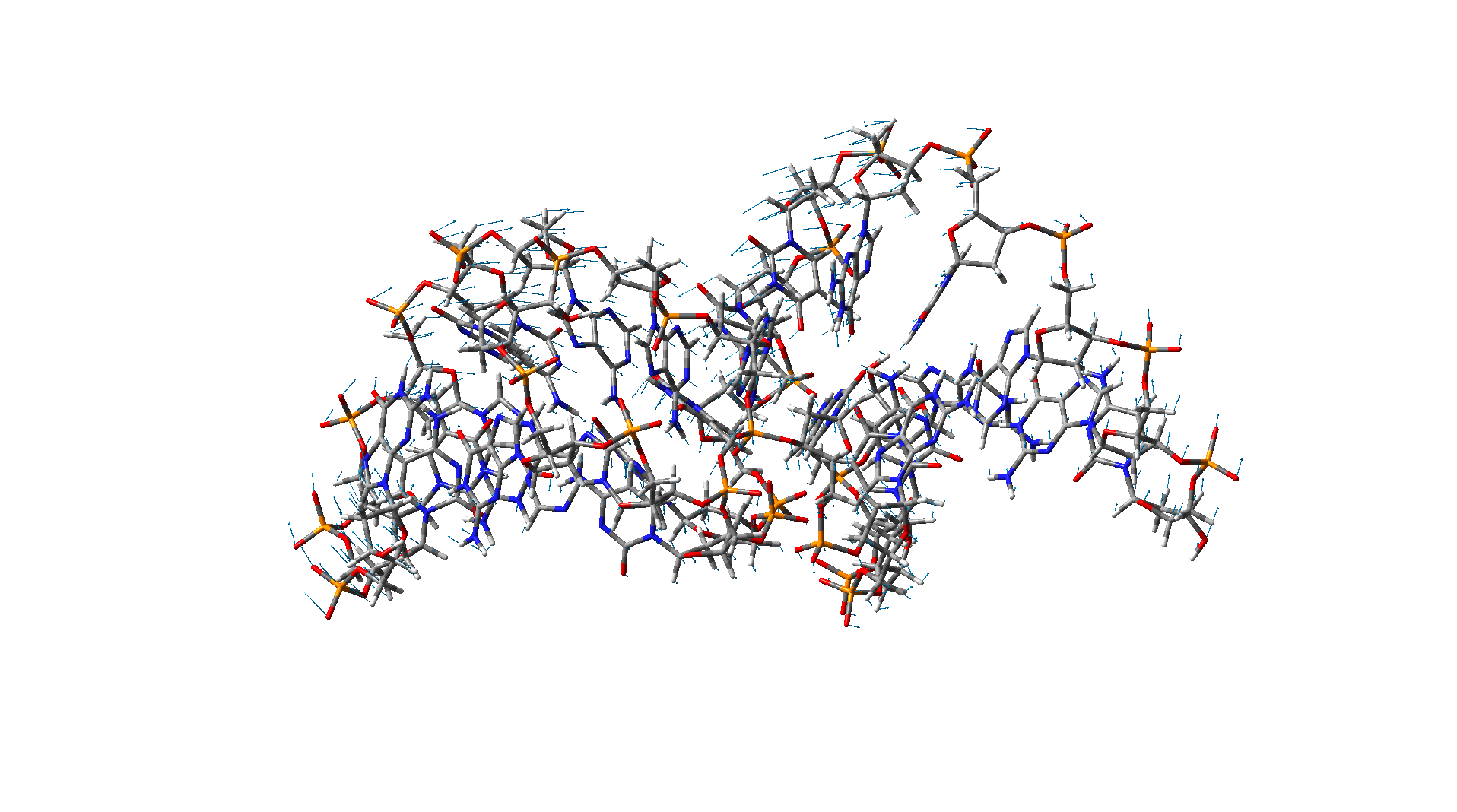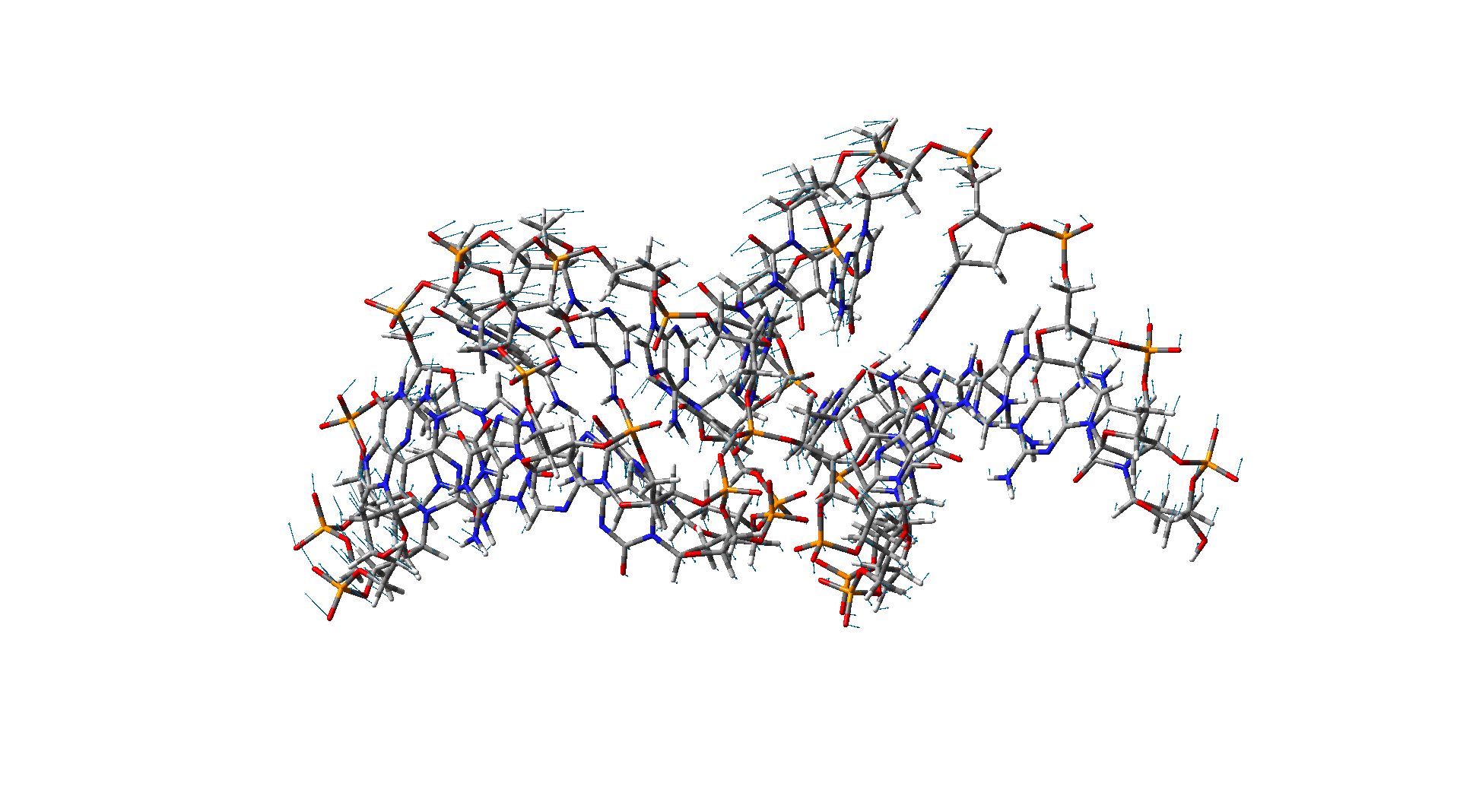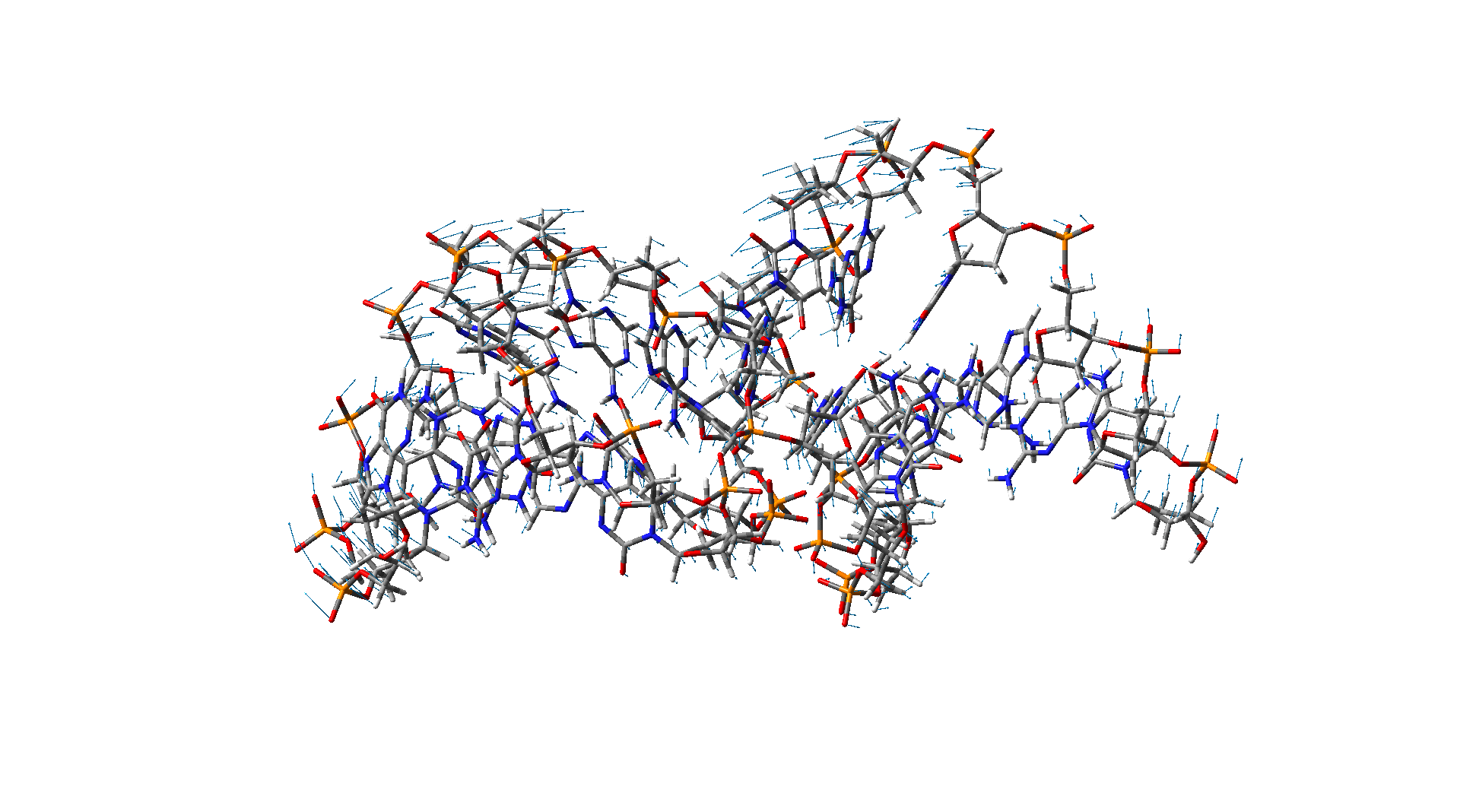 Bending mode of a DNA Bending mode of a DNA |
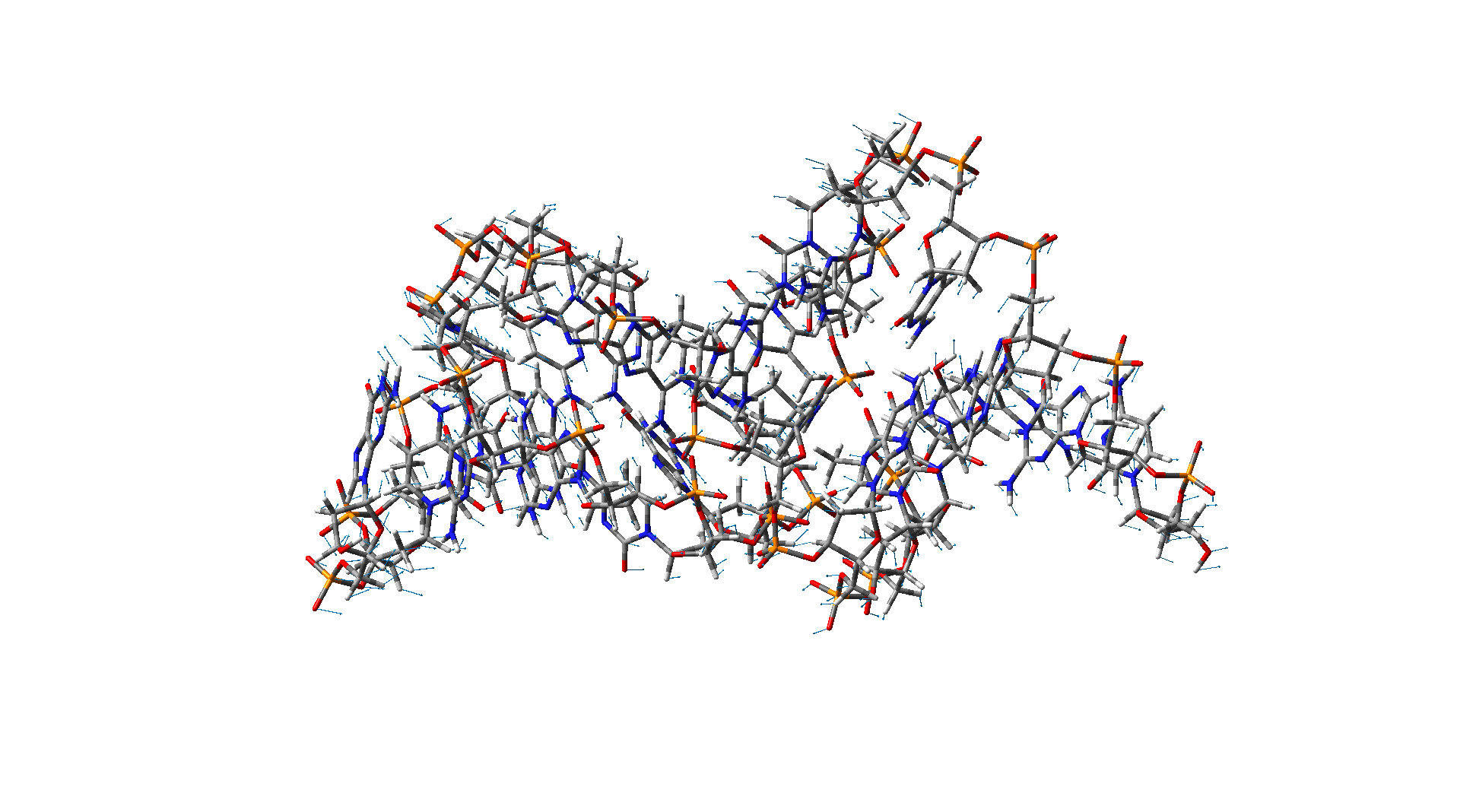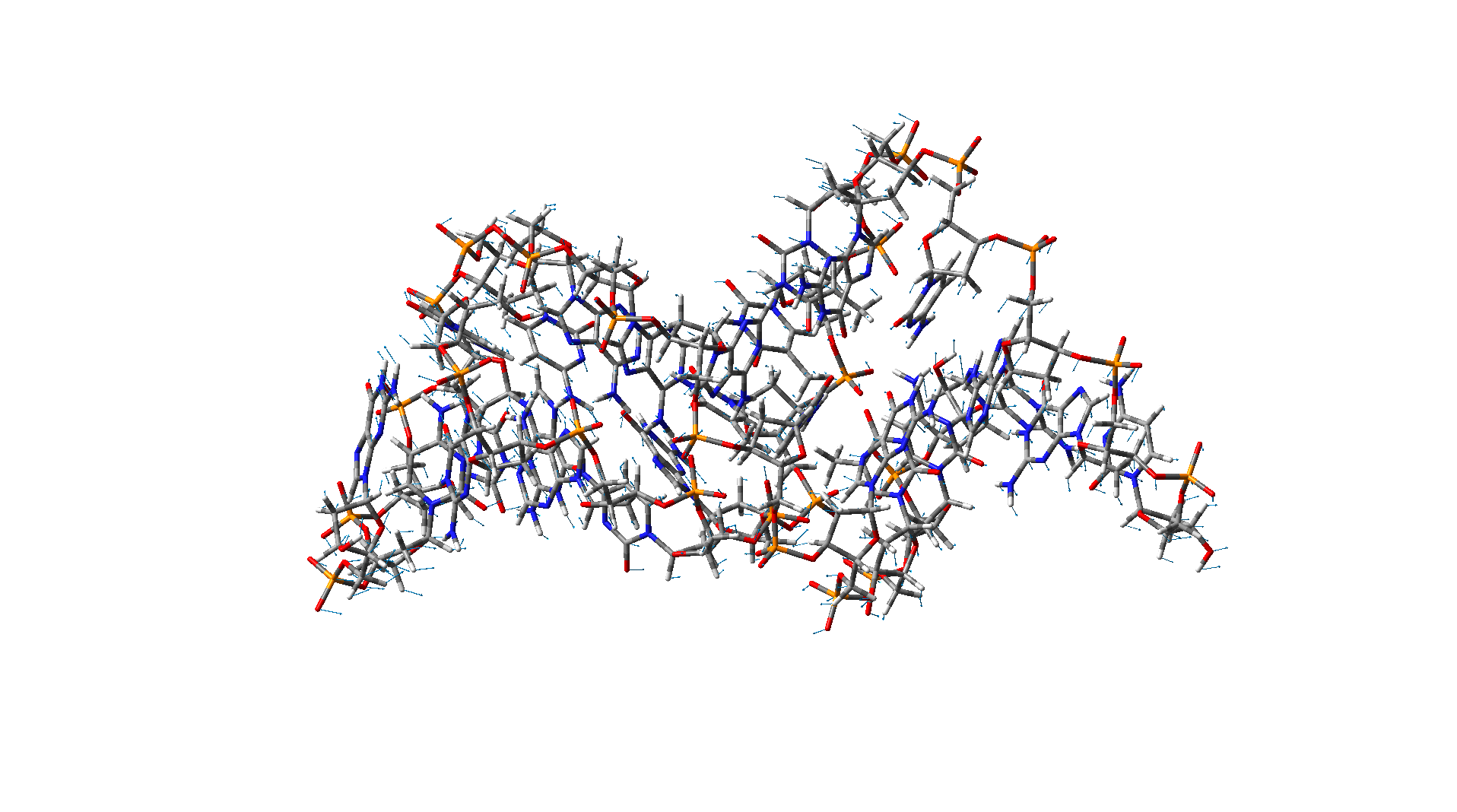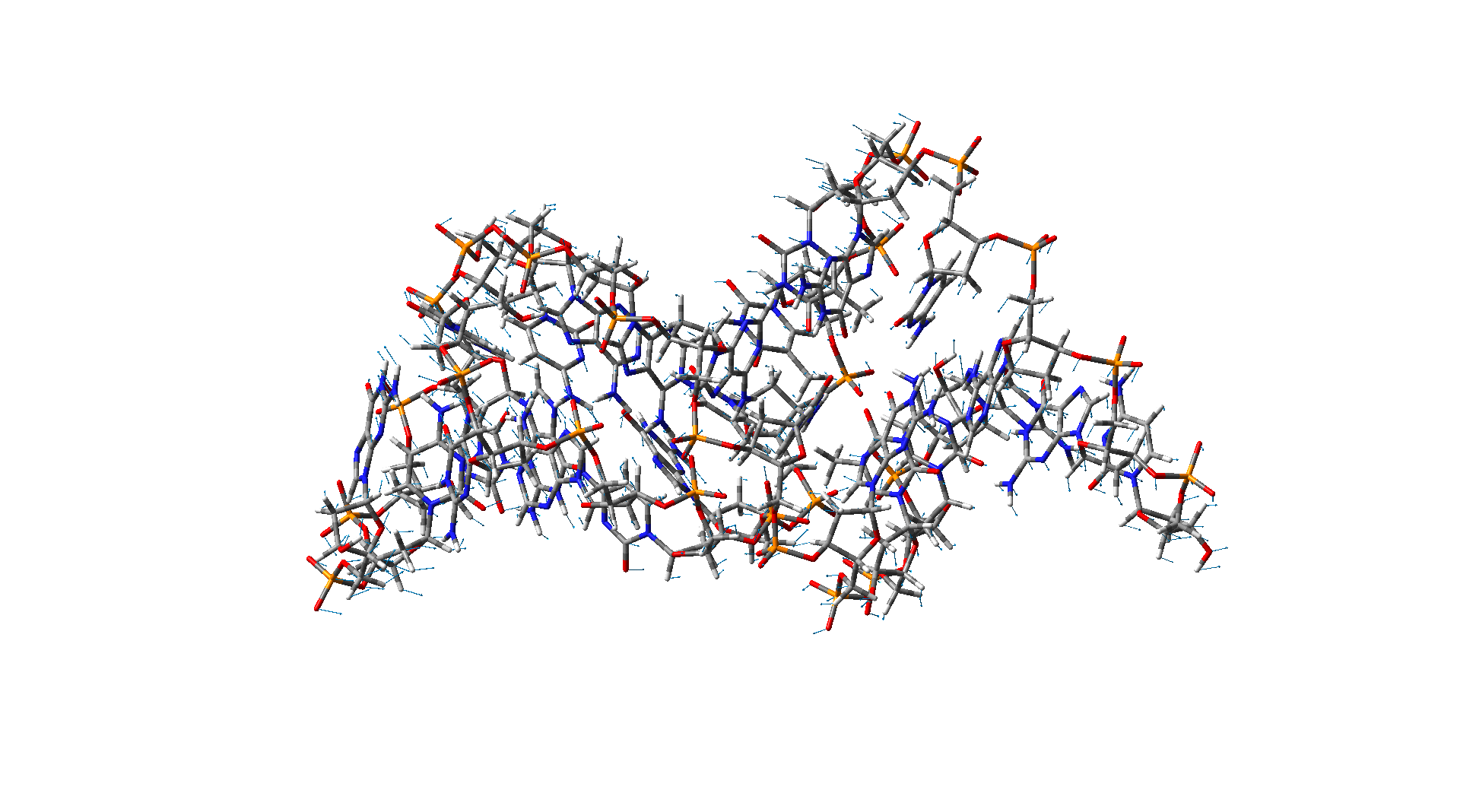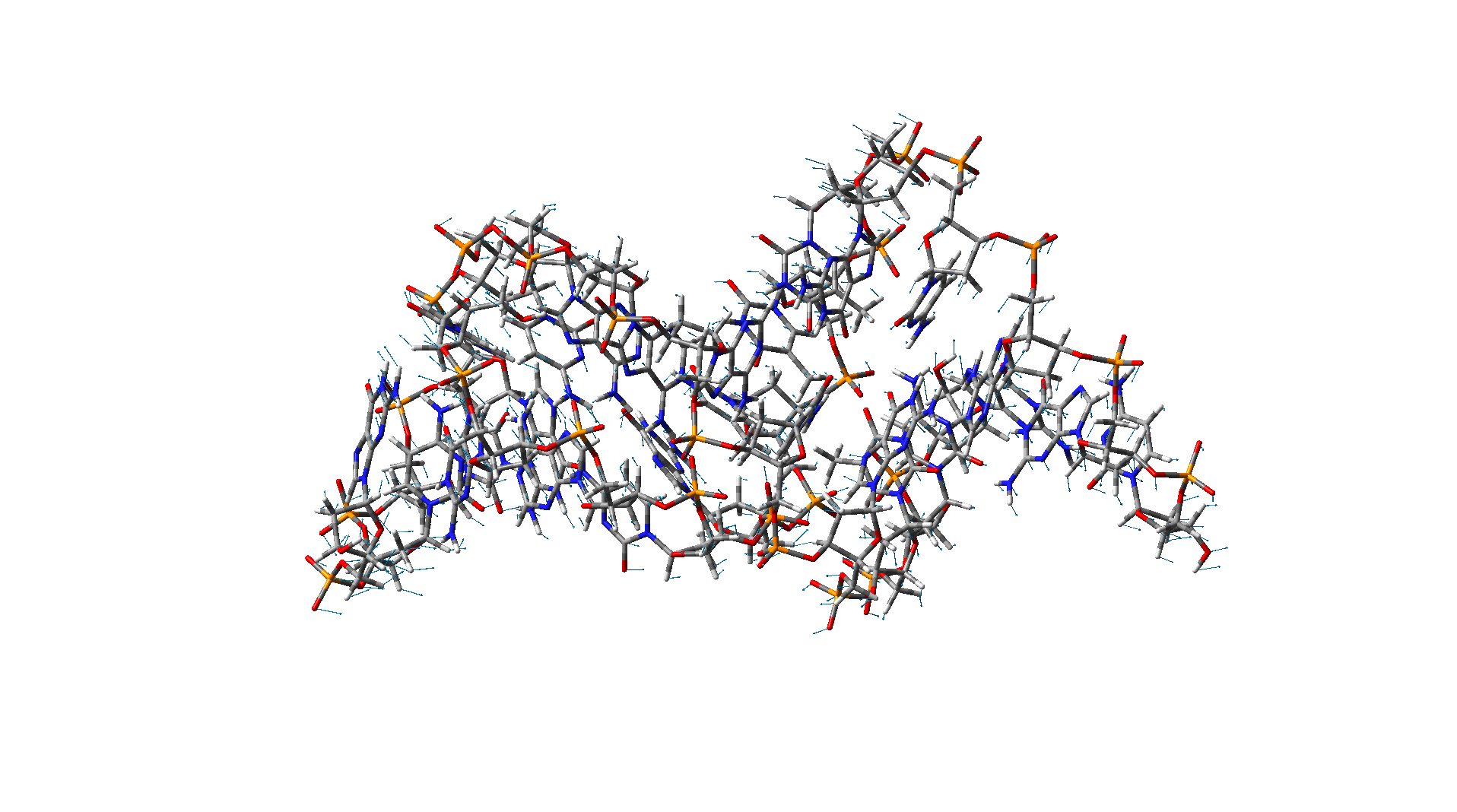 Torsional-like mode of a DNA Torsional-like mode of a DNA |
These two figures show different vibration modes of a DNA nanotube with 15 base pairs. The results are obtained using the molecular dynamic simulation.
 Axial vibration mode of a ZnO nanotube Axial vibration mode of a ZnO nanotube |
 Bending vibration mode of a ZnO nanotube Bending vibration mode of a ZnO nanotube |
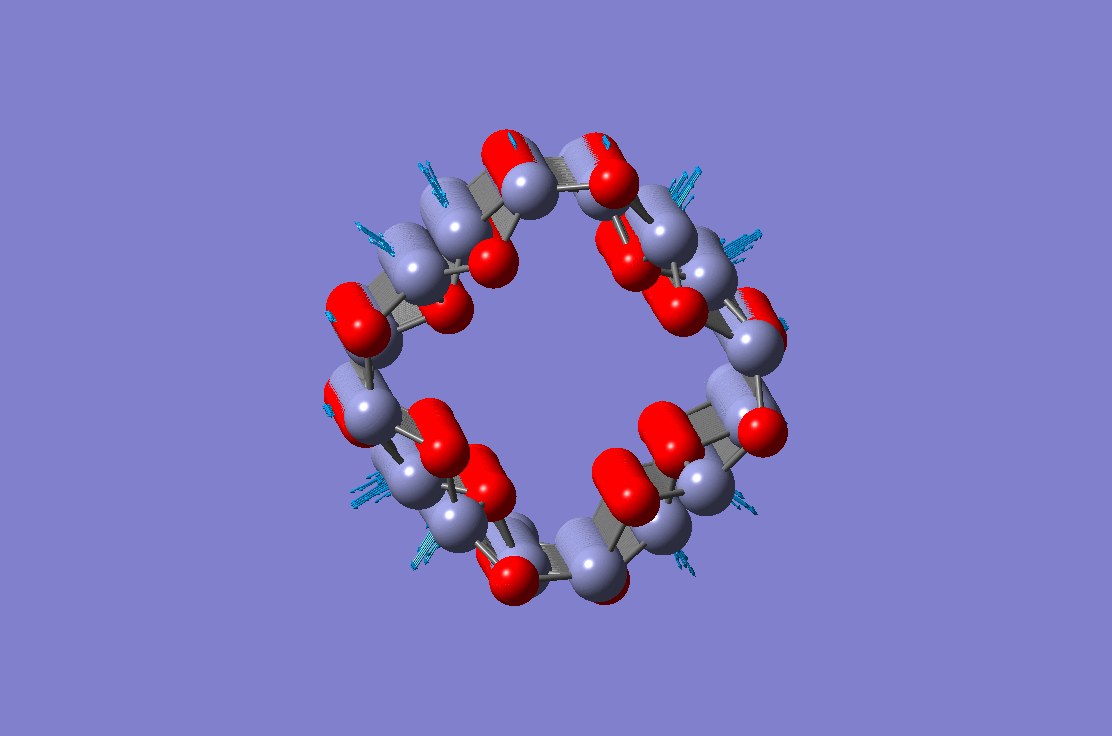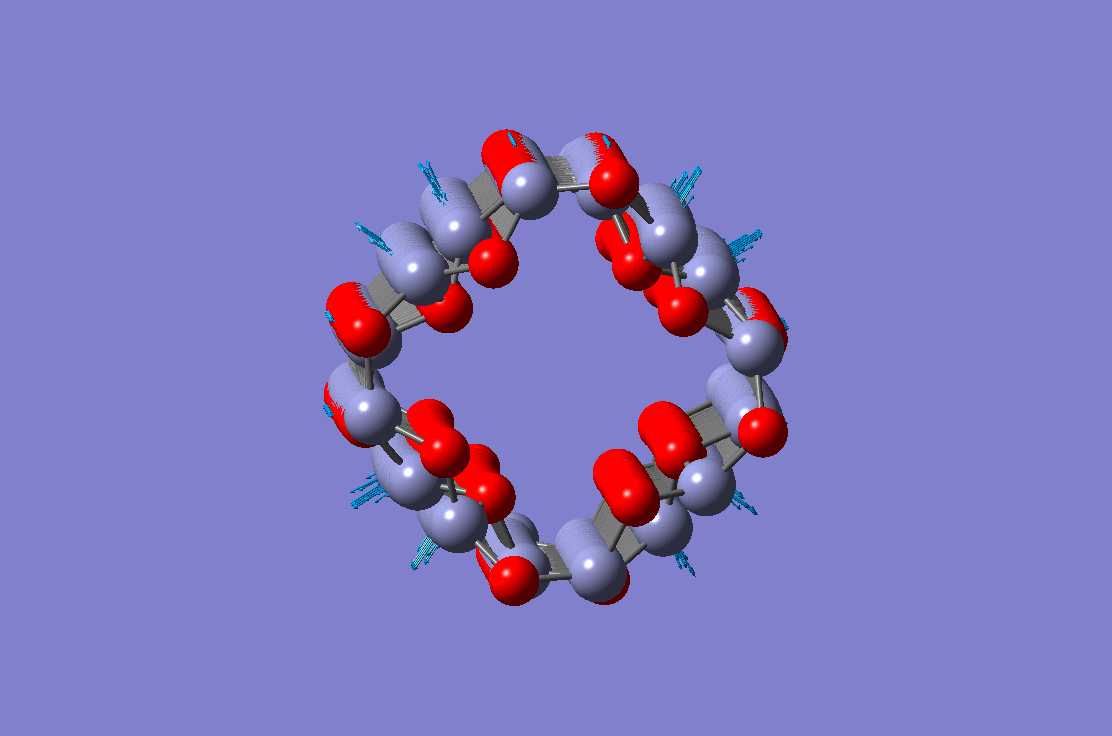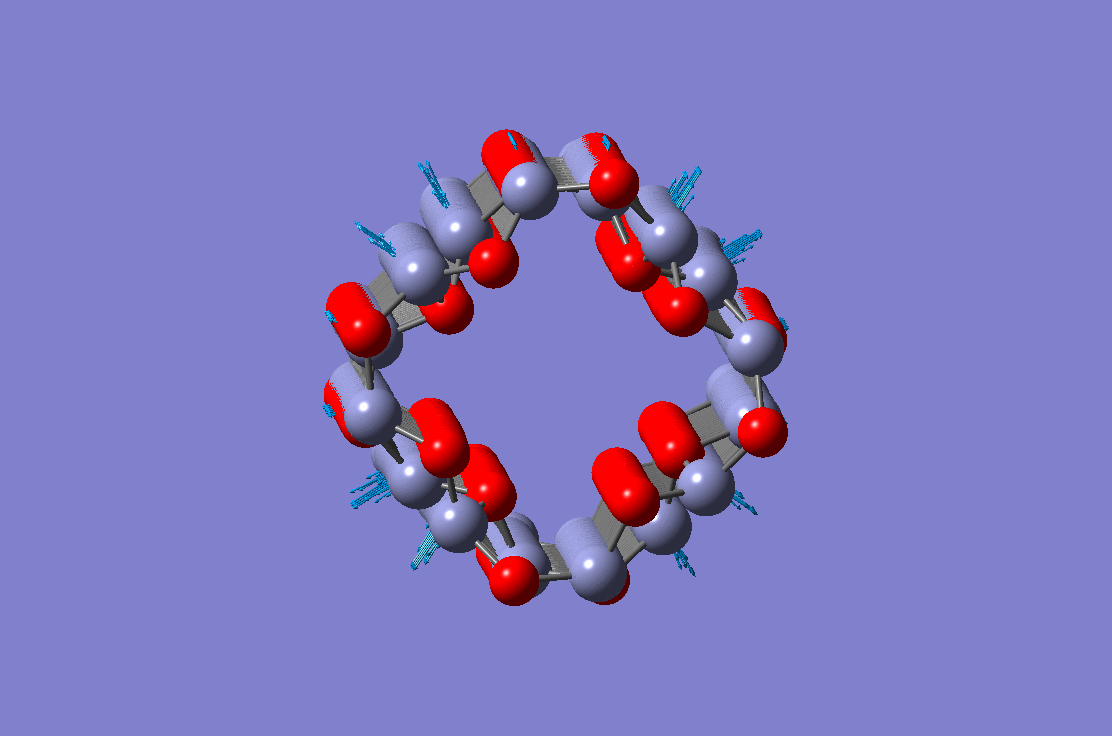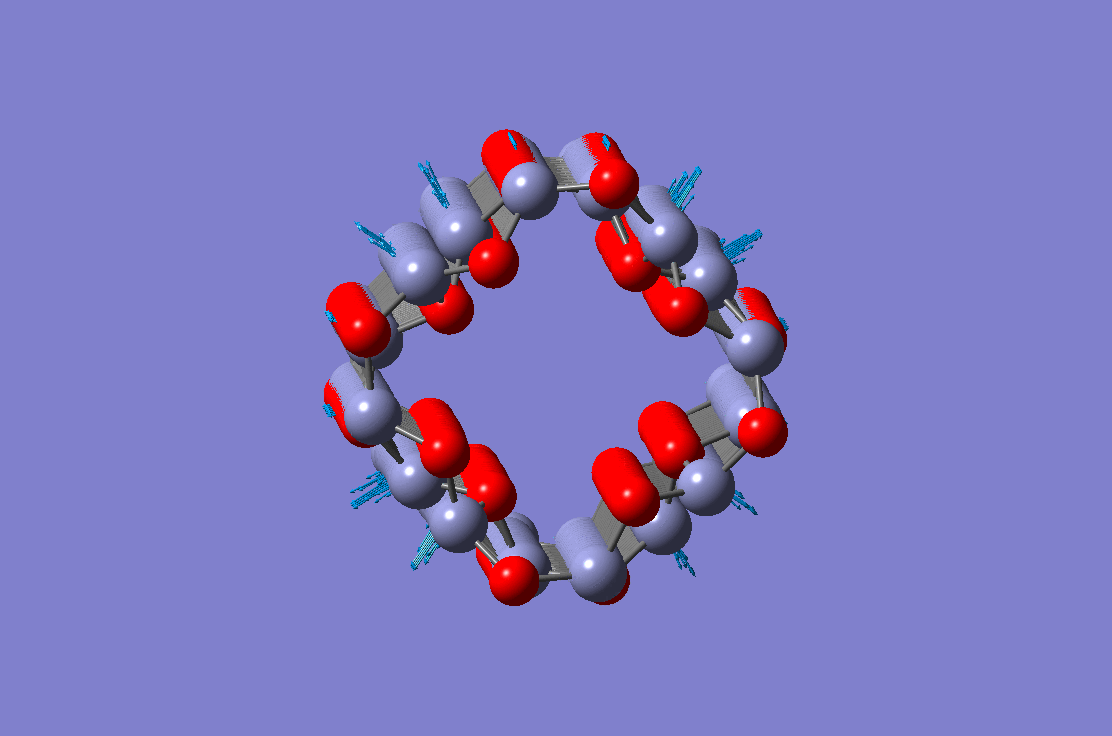 Radial breathing mode of a ZnO nanotube Radial breathing mode of a ZnO nanotube |
 Torsional vibration mode of a ZnO nanotube Torsional vibration mode of a ZnO nanotube |
These four figures show different vibration modes of a ZnO nanotube. The results are obtained using the molecular dynamic simulation. Equivalent continuum and finite element based theory have been developed and validated against molecular dynamic simulations.
Key Journal Publications
- Chandra, Y., Flores, E. I. S., Scarpa, F., and Adhikari, S., “Buckling of hybrid nanocomposites with embedded graphene and carbon nanotubes,” Physica E: Low-dimensional Systems and Nanostructures, Vol. 83, No. 9, 2016, pp. 434-441.
- Chandra, Y., Scarpa, F., Adhikari, S., Zhang, J., Flores, E. S., and Peng, H.-X., “Pullout strength of graphene and carbon nanotube/epoxy composites,” Composites Part B: Engineering, Vol. 102, No. 10, 2016, pp. 1-8.
- Flores, E. I. S., Ajaj, R. M., Adhikari, S., Dayyani, I., and Castro-Triguero, R., “Hyperelastic tension of graphene,” Applied Physics Letters, Vol. 106, No. 6, 2015, pp. 061901:1-4.
- Flores, E. I. S., Adhikari, S., Friswell, M. I., and Scarpa, F., “A hybrid atomistic approach for the mechanics of deoxyribonucleic acid molecules,” ASME Journal of Nanotechnology in Engineering and Medicine, Vol. 4, No. 4, 2013, pp. 041006:1-7.
- Zhang, J., Wang, C. W., and Adhikari, S., “Surface effects on the electrostatic potential generated in a bent gallium nitride nanowire,” IEEE Transactions on Nanotechnology,Vol. 13, No. 3, 2014, pp. 600-606.
- Zhang, J., Wang, C. W., and Adhikari, S., “Fracture and buckling of piezoelectric nanowires subject to an electric field,” Journal of Applied Physics, Vol. 114, No. 17, 2013, pp. 174306:1-7.
- Zhang, J., Wang, C. W., and Adhikari, S., “Molecular structure-dependent deformations in boron nitride nanostructures subject to an electrical filed,” Journal of Physics D: Applied Physics, Vol. 46, No. 23, 2013, pp. 235303:1-6.
- Zhang, J., Wang, C. W., Chowdhury, R., and Adhikari, S., “Size and temperature dependent elastic and piezoelectric properties of gallium nitride nanobelts,” Scripta Materialia, Vol. 68, No. 8, 2013, pp. 627-630.
- Chandra, Y., Scarpa, F., Chowdhury, R., Adhikari, S., and Seinz, J., “Multiscale hybrid atomistic-FE approach for the nonlinear tensile behaviour of graphene nanocomposites,” Composites Part A: Applied Science and Manufacturing, Vol. 46, No. 3, 2013, pp. 147-153.
- Zhang, J., Wang, C. W., Chowdhury, R., and Adhikari, S., “Small-scale effect on the mechanical properties of metallic nanotubes,” Applied Physics Letters, Vol. 101, No. 9, 2012, pp. 093109:1-4.
- Murmu, T., Seinz, J., Adhikari, S., and Arnold, C., “Nonlocal buckling of double-nanoplate-systems under biaxial compression,” Composites Part B, Vol. 45, No. 1, 2013, pp. 84-94.
- Zhang, J., Wang, C. W., and Adhikari, S., “Surface effect on the buckling of piezoelectric nanofilms,” Journal of Physics D, Vol. 45, No. 28, 2012, pp. 285301:1-8.
- Chandra, Y., Chowdhury, R., Scarpa, F., Adhikari, S., Seinz, J., Arnold, C., Murmu, T., and Bould, D., “Vibration frequency of graphene based composites: A multiscale approach,” Materials Science and Engineering B, Vol. 177, No. 3, 2012, pp. 303-310.
- Boldrin, L., Scarpa, F., Chowdhury, R., Adhikari, S., and Ruzzene, M., “Effective mechanical properties of hexagonal boron nitride nanosheets,” Nanotechnology, Vol. 22, No. 50, 2011, pp. 505702:1-7.
- Murmu, T., Seinz, J., Adhikari, S., and Arnold, C., “Nonlocal buckling behaviour of bonded double-nanoplate-system,” Journal of Applied Physics, Vol. 110, No. 8, 2011, pp. 084316:1-8.
- Flores, E. I. S., Adhikari, S., Friswell, M. I., and Scarpa, F., “Hyperelastic axial buckling of single wall carbon nanotubes,” Physica E: Low-dimensional Systems and Nanostructures, Vol. 44, No. 2, 2011, pp. 525-529.
- Chandra, Y., Chowdhury, R., Adhikari, S., and Scarpa, F., “Elastic instability of bilayer graphene using atomistic finite element,” Physica E: Low-dimensional Systems and Nanostructures, Vol. 44, No. 1, 2011, pp. 12-16.
- Scarpa, F., Chowdhury, R., Kam, K., Adhikari, S., and Ruzzene, M., “Dynamics of mechanical waves in periodic graphene nanoribbon assemblies,” Nanoscale Research Letters, Vol. 6, 2011, pp. 430:1-10.
- Chandra, Y., Chowdhury, R., Scarpa, F., and Adhikari, S., “Vibrational characteristics of bilayer graphene sheets,” Thin Solid Films, Vol. 519, No. 18, 2011, pp. 6026-6032.
- Scarpa, F., Chowdhury, R., and Adhikari, S., “Thickness and in-plane elasticity of Graphane,” Physics Letters A, Vol. 375, No. 20, 2011, pp. 2071-2074.
- Flores, E. I. S., Adhikari, S., Friswell, M. I., and Scarpa, F., “Hyperelastic finite element model for single wall carbon nanotubes in tension,” Computational Materials Science, Vol. 50, No. 3, 2011, pp. 1083-1087.
- Scarpa, F., Adhikari, S., and Phani, A., “Auxeticity in single layer graphene sheets,” International Journal of Novel Materials, Vol. 1, No. 2, 2010, pp. 39-43.
- Scarpa, F., Peng, H. X., Boldri, L., Remillat, C. D. L., and Adhikari, S., “Coupled thermo-mechanics of single-wall carbon nanotubes,” Applied Physics Letters, Vol. 97, No. 15, 2010, pp. 151903.
- Chowdhury, R., Adhikari, S., and Rees, P., “Optical properties of silicon doped ZnO,” Physica B: Condensed Matter, Vol. 405, No. 23, 2010, pp. 4763-4767.
- Chowdhury, R., Adhikari, S., Wang, C. Y., and Scarpa, F., “A molecular mechanics approach for the vibration of single walled carbon nanotubes,” Computational Materials Science, Vol. 48, No. 4, 2010, pp. 730-735.
- Chowdhury, R., Adhikari, S., and Scarpa, F., “Elasticity and piezoelectricity of zinc oxide nanostructure,” Physica E: Low-dimensional Systems and Nanostructures, Vol. 42, No. 8, 2010, pp. 2036-2040.
- Scarpa, F., Adhikari, S., and Chowdhury, R., “The transverse elasticity of bilayer graphene,” Physics Letters A, Vol. 374, No. 19-20, April 2010, pp. 2053-2057.
- Scarpa, F., Adhikari, S., Gil, A. J., and Remillat, C., “The bending of single layer graphene sheets: Lattice versus continuum approach,” Nanotechnology, Vol. 20, No. 12, 2010, pp. 085405.
- Chowdhury, R., Rees, P., Adhikari, S., Scarpa, F., and Wilks, S., “Electronic Structures of Silicon doped ZnO,” Physica B: Condensed Matter, Vol. 405, No. 8, April 2010, pp. 1980-1985.
- Scarpa, F., Adhikari, S., and Wang, C. Y., “Nanocomposites with auxetic nanotubes,” International Journal of Smart and Nanomaterials, Vol. 1, No. 2, 2010, pp. 83-94.
- Scarpa, F., Adhikari, S., and Wang, C. Y., “Mechanical properties of non reconstructed defective single wall carbon nanotubes,” Journal of Physics D: Applied Physics, Vol. 42, No. 085306, 2009, pp. 1-6.
- Scarpa, F., Adhikari, S., and Phani, A., “Effective mechanical properties of single graphene sheets,” Nanotechnology, Vol. 20, January 2009, pp. 065709:1-11.
A.5. Structural dynamics using continuum theory
The theory of continuum mechanics plays a pivotal role in the analysis and design of macroscopic systems. The purpose of this research is to investigate its applicability for nano-nano-scale structures. We use the theory of Euler-Bernoulli beams, Timoshenko beams, bars, thin plates, hollow spheres, spherical shells and hollow cylinders. Closed-form analytical results are compared with the more detailed finite element and molecule mechanics simulation results. Our closed-form results provide unique physical understandings.
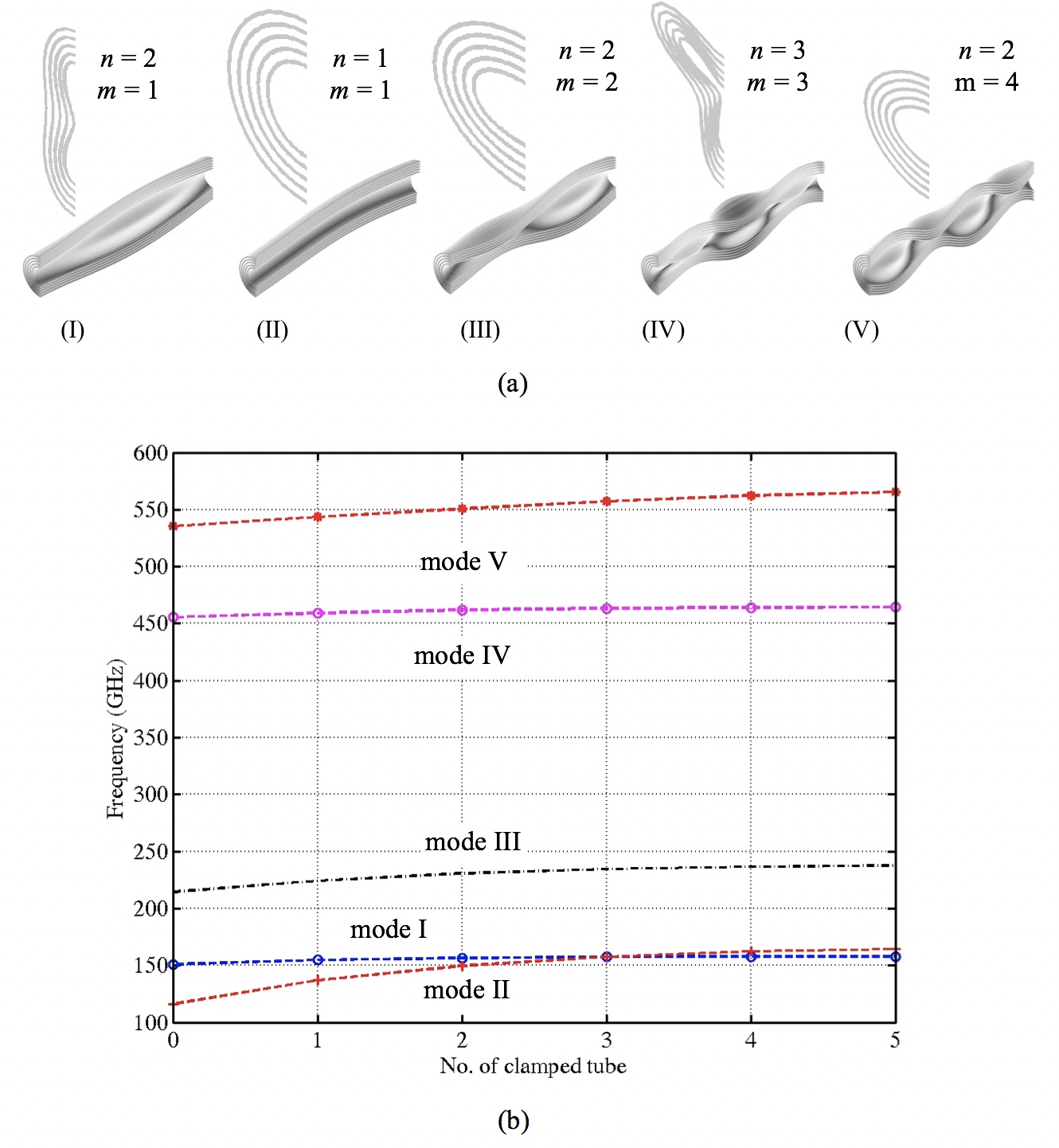 The five low frequency vibration modes of a multi-walled CNT The five low frequency vibration modes of a multi-walled CNT |
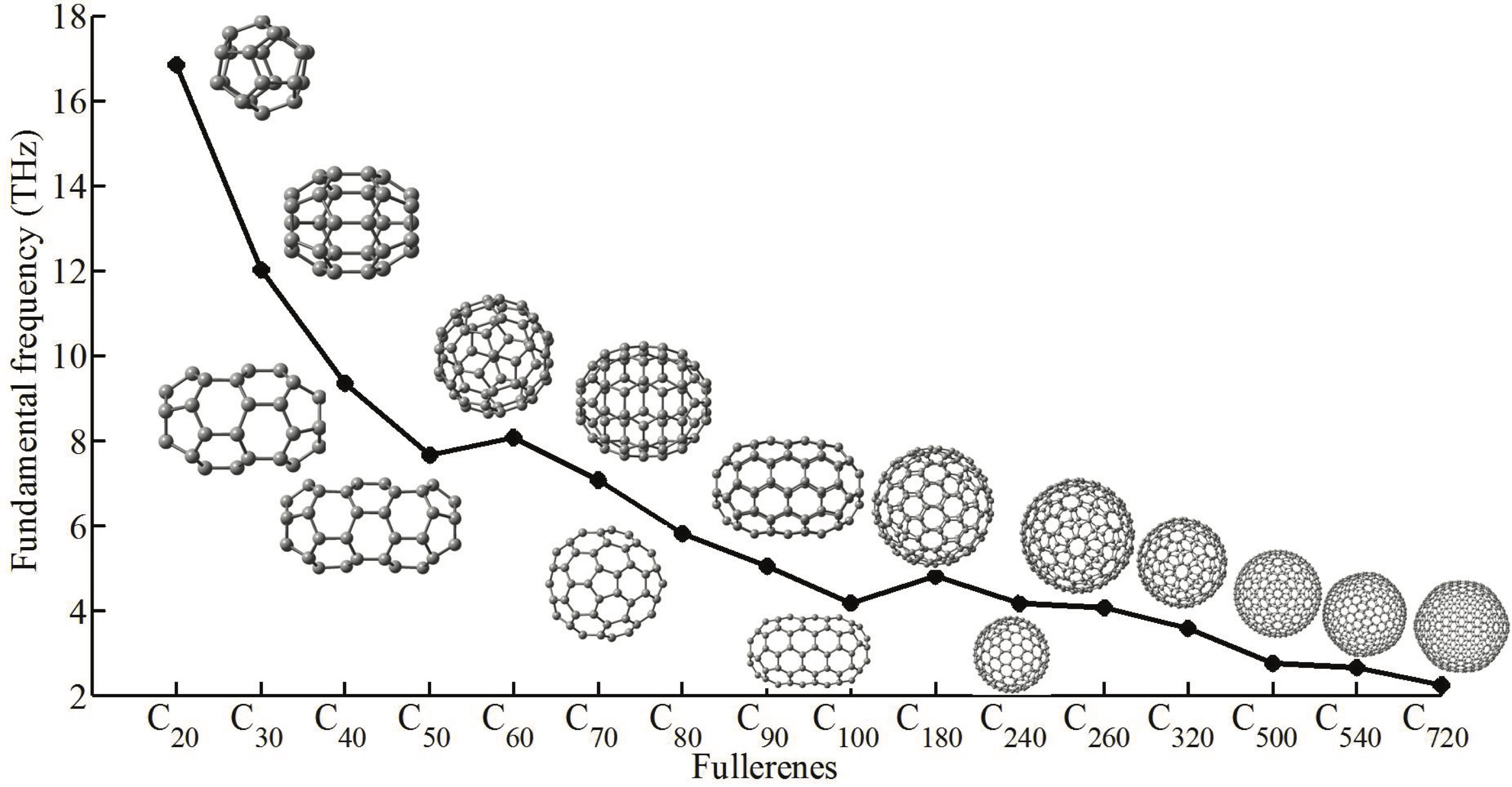 The variation of the first natural frequency across the complete range of fullerenes The variation of the first natural frequency across the complete range of fullerenes |
Key Journal Publications
- Adhikari, S. and Chowdhury, R., “Vibration spectra of fullerene family,” Physics Letters A, Vol. 375, No. 22, 2011, pp. 1276-1280.
- Wang, C. W. and Adhikari, S., “ZnO-CNT composite nanowires as nanoresonators,” Physics Letters A, Vol. 375, No. 22, 2011, pp. 2171-2175.
- Chowdhury, R., Adhikari, S., Scarpa, F., and Friswell, M. I., “Transverse vibration of single layer graphene sheets,” Journal of Physics D: Applied Physics, Vol. 44, No. 20, 2011, pp. 205401:1-11.
- Chowdhury, R., Adhikari, S., and Scarpa, F., “Vibrational analysis of ZnO nanotubes: A molecular mechanics approach,” Applied Physics A, Vol. 102, No. 2, 2011, pp. 301-308.
- Chowdhury, R., Wang, C. Y., Adhikari, S., and Scarpa, F., “The vibration of boron nitride nanotubes,” Nanotechnology, Vol. 20, No. 12, 2010, pp. 365702:1-9.
- Wang, C. Y., Zhao, Y., Adhikari, S., and Feng, Y. T., “Vibration of axially strained triple-wall carbon nanotubes,” Journal of Computational and Theoretical Nanoscience,Vol. 7, No. 11, 2010, pp. 2176-2185.
- Chowdhury, R., Wang, C. Y., Adhikari, S., and Tong, F. M., “Sliding oscillations of multiwall carbon nanotubes,” Physica E: Low-dimensional Systems and Nanostructures,Vol. 42, No. 9, 2010, pp. 2295-2300.
- Wang, C. Y., Li, C. F., and Adhikari, S., “Axisymmetric vibration of singlewall carbon nanotubes in water,” Physics Letters A, Vol. 374, No. 24, 2010, pp. 2467-2474.
- Gil, A. J., Adhikari, S., Scarpa, F., and Bonet, J., “The wrinkling of single-layer graphene sheets,” Journal of Physics: Condensed Matter, Vol. 22, No. 14, 2010, pp. 145302.
- Chowdhury, R., Wang, C. Y., and Adhikari, S., “Low frequency vibration of multiwall carbon nanotubes with heterogeneous boundaries,” Journal of Physics D: Applied Physics,Vol. 43, No. 085405, 2010, pp. 1-8.
- Wang, C. Y., Li, C. F., and Adhikari, S., “Dynamic behaviors of microtubules in cytosol,” Journal of Biomechanics, Vol. 42, No. 9, August 2009, pp. 1270-1274.
- Tong, F. M., Wang, C. Y., and Adhikari, S., “Axial buckling of multiwall carbon nanotubes with heterogeneous boundary conditions,” Journal of Applied Physics,Vol. 105, May 2009, pp. 094325:1-7.
- Scarpa, F. and Adhikari, S., “Uncertainty modelling of carbon nanotube terahertz oscillators,” Journal of Non-Crystalline Solids, Vol. 354, No. 35-39, October 2008, pp. 4151-4156.
- Scarpa, F. and Adhikari, S., “A mechanical equivalence for the Poisson’s ratio and thickness of C-C bonds in single wall carbon nanotubes,” Journal of Physics D: Applied Physics, Vol. 41, No. 085306, 2008, pp. 1-5.
Home|
Research|
Publications|
Teaching|
Lectures|
Students and Post-docs|
Education & awards|
Professional activities|
Contact|
Departmental web page|
Downloads
This page was by Sondipon Adhikari
|


 Three main types of mechanical metamaterials
Three main types of mechanical metamaterials An example of a disordered cellular metamaterial (hexagonal unit cells)
An example of a disordered cellular metamaterial (hexagonal unit cells) General approaches employed to model and study nanostructures
General approaches employed to model and study nanostructures Extrinsic lengths in the plates of different scale
Extrinsic lengths in the plates of different scale
 Armchair double-walled carbon nanotube subjected to axial magnetic field
Armchair double-walled carbon nanotube subjected to axial magnetic field Axial magnetic field exerted on multiple SWCNTs embedded in polymer matrix
Axial magnetic field exerted on multiple SWCNTs embedded in polymer matrix Bending mode of a DNA
Bending mode of a DNA Torsional-like mode of a DNA
Torsional-like mode of a DNA Axial vibration mode of a ZnO nanotube
Axial vibration mode of a ZnO nanotube Bending vibration mode of a ZnO nanotube
Bending vibration mode of a ZnO nanotube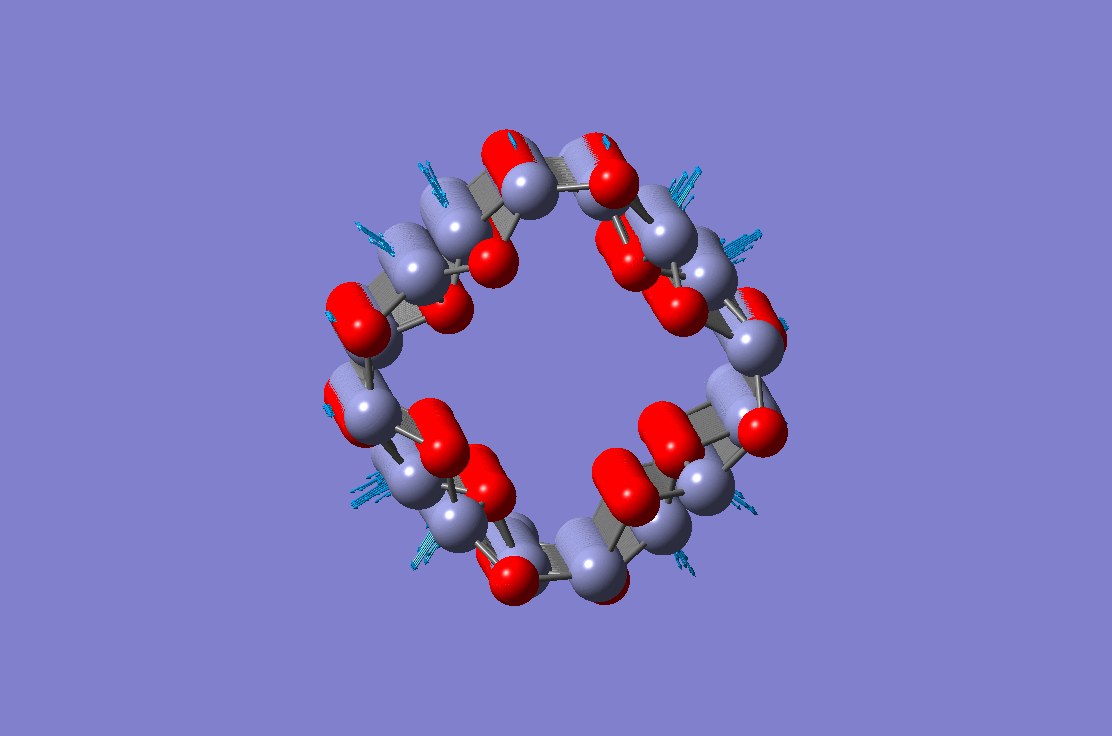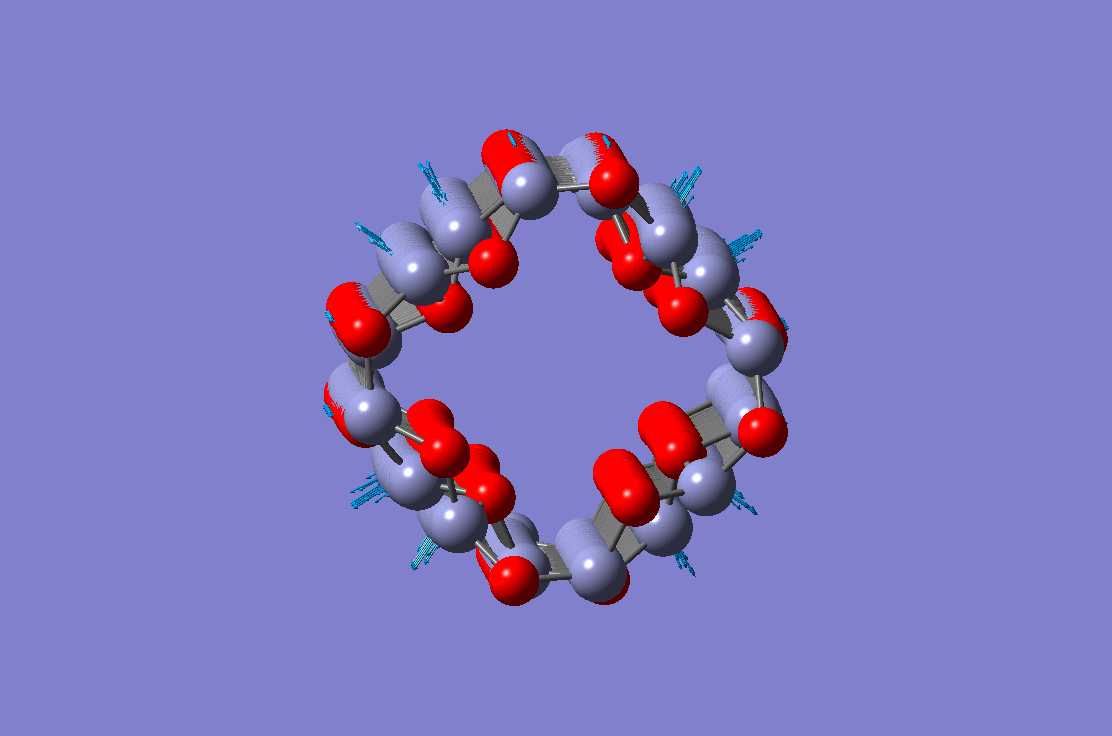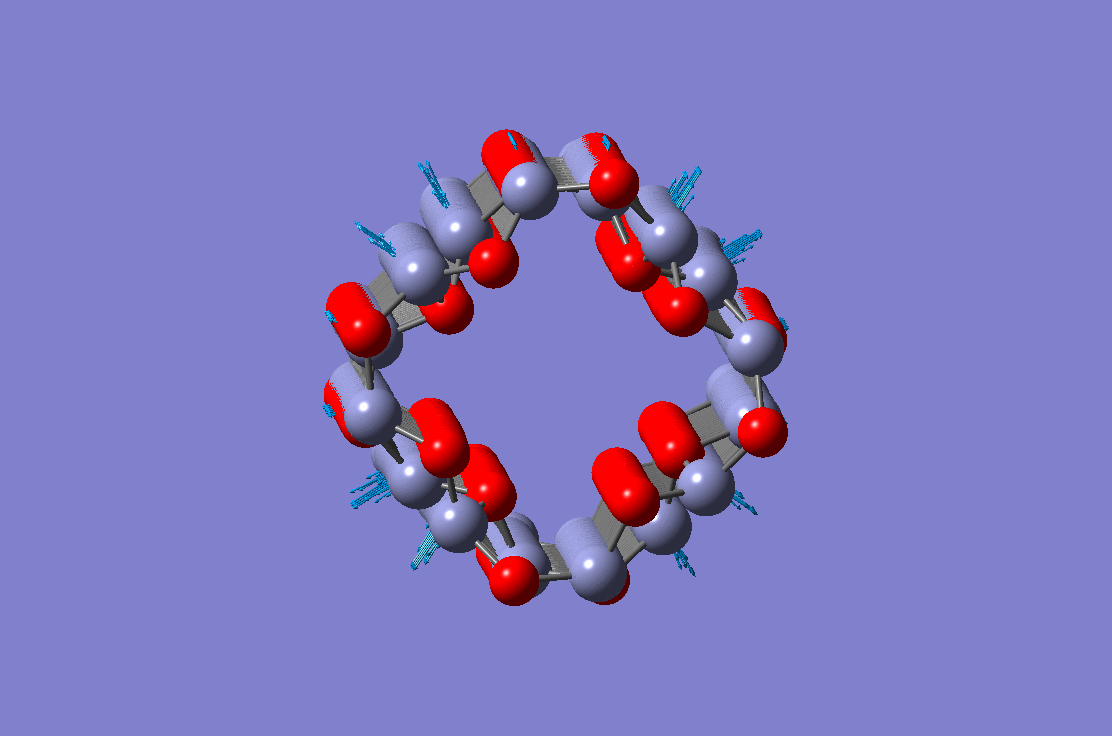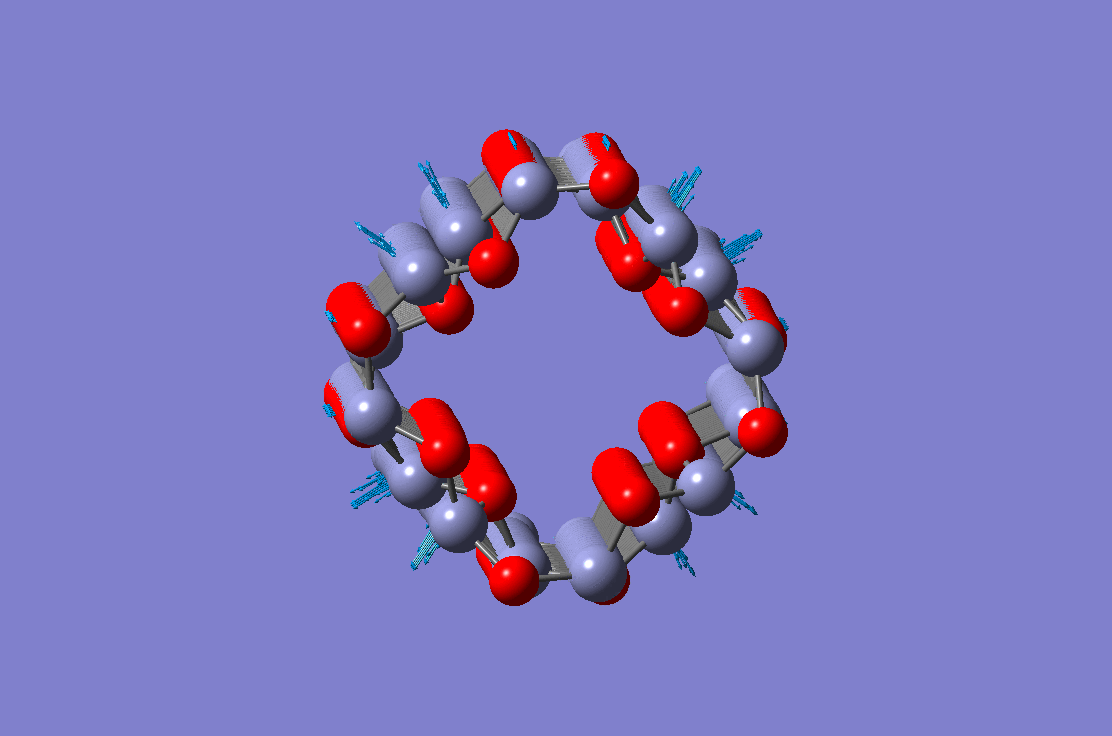 Radial breathing mode of a ZnO nanotube
Radial breathing mode of a ZnO nanotube Torsional vibration mode of a ZnO nanotube
Torsional vibration mode of a ZnO nanotube The five low frequency vibration modes of a multi-walled CNT
The five low frequency vibration modes of a multi-walled CNT The variation of the first natural frequency across the complete range of fullerenes
The variation of the first natural frequency across the complete range of fullerenes